link : http://www.videotutorialsrock.com/opengl_tutorial/terrain/text.php
Representing and Loading 3D Terrains
게임 및 기타 3D 프로그램의 한 가지 일반적인 기능은 3D 지형이 있다는 것이다. 이 강의에서는 다음 지형을 작성한다:

문제는 지형을 어떻게 표현할 것인가이다. 가장 직접적이고 좋은 방법 중 하나는 x-z 평면에 2D 그리드를 만들고, 각 그리드 지점에
지형의 높이를 저장하는 것이다. 이것은 우리가 모든 지형을 만들지 못하게한다. 예를 들어, 순수한 수직 벽이나 "뒤로" 기울어진
벽을 가질 수는 없다. 그러나 여전히 우리는 많은 것을 이를 통해 만들 수 있다.
모든 높이를 프로그램 자체에 하드 코딩 할 수 있다. 그러나 높이를 별도의 파일에 저장하는 것이 좋다. 우리가 사용할 수 있는 가장
직접적인 유형의 파일은 회색 음영 이미지이다. 여기서 흰색은 최대 허용 높이를 나타내고 검은 색은 허용 가능한 최소 높이를 나타낸다.
이러한 이미지 파일을 "heightmap"이라고 한다. 이것은 또한 좋은 아이디어로 밝혀졌따. 하나는 3D로 렌더링하지 않고도 지형의 모습을
볼 수 있다. 아래는 프로그램에 대한 heightmap의 확대 버전이다:

비록 내가 그것들에 너무 친숙하지는 않지만, heightmap을 만들고 조작하기 위한 툴이 있다. 그렇다면 이 heightmap을 어떻게 만들었을까?
그건 내 비밀이다. (어쩌라는건지...?)
Going Through The Code
우리 프로그램이 어떻게 지형을 로드하고 표시하는지 보도록 하겠다. 맨 위에는 "vec3f.h"가 include 되어있다. 여기에는 세 개의 부동 소수점
벡터인 "Vec3f"라는 특수한 벡터 클래스가 포함된다. 벡터가 기대하는 모든 것을 한다. 당신은 +와 -를 사용해 더하기와 빼기를 할 수 있으며,
vec[0], vec[1], vec[2]를 사용해 *와 /를 사용해 곱셈과 나눗셈을 하고, 그 밖의 것들을 할 수 있다. Vec3f를 적용 할 수도 있다. vec3f.h를 보고
Vec3f로 할 수 있는 모든 것을 볼 수 있다. Vec3f 클래스를 사용해 법선 벡터를 저장한다.
//Represents a terrain, by storing a set of heights and normals at 2D locations class Terrain { private: int w; //Width int l; //Length float** hs; //Heights Vec3f** normals; bool computedNormals; //Whether normals is up-to-date
여기에 우리의 지형 클래스가 있다. 폭과 길이를 저장하며 x와 z방향으로 격자 점의 수를 나타낸다. 2차원 배열을 사용해 각 점에서
가장 모든 높이와 법선을 저장한다. 마지막으로, 법선 배열에 실제로 올바른 법선이 있는지 여부를 알려주는 bool이 있다.
먼저 모든 높이를 설정한 다음 모든 법선을 한꺼번에 계산해야하므로 법선이 아직 계산되지 않았을 수 있다.
Terrain(int w2, int l2) { w = w2; l = l2; hs = new float*[l]; for(int i = 0; i < l; i++) { hs[i] = new float[w]; } normals = new Vec3f*[l]; for(int i = 0; i < l; i++) { normals[i] = new Vec3f[w]; } computedNormals = false; }
다음은 Terrian 클래스의 생성자이다. 모든 변수를 초기화한다.
~Terrain() { for(int i = 0; i < l; i++) { delete[] hs[i]; } delete[] hs; for(int i = 0; i < l; i++) { delete[] normals[i]; } delete[] normals; }
다음은 Terrian 클래스의 소멸자이다. 소멸자는 2차원 배열 hs와 법선을 삭제한다.
int width() { return w; } int length() { return l; }
지형의 너비와 길이를 반환하는 메소드이다.
//Sets the height at (x, z) to y void setHeight(int x, int z, float y) { hs[z][x] = y; computedNormals = false; } //Returns the height at (x, z) float getHeight(int x, int z) { return hs[z][x]; }
이 메소드를 사용하면 특정 격자점에서 지형의 높이를 설정하고 가져올 수 있다.
//Computes the normals, if they haven't been computed yet void computeNormals() { //... }
이 메소드는 각 점에서 법선을 계산한다. 이따가 다시 볼 것이다.
//Returns the normal at (x, z) Vec3f getNormal(int x, int z) { if (!computedNormals) { computeNormals(); } return normals[z][x]; } };
여기에는 어떤 점에서 법선을 반환하는 메소드가 있다.
//Loads a terrain from a heightmap. The heights of the terrain range from //-height / 2 to height / 2. Terrain* loadTerrain(const char* filename, float height) { Image* image = loadBMP(filename); Terrain* t = new Terrain(image->width, image->height); for(int y = 0; y < image->height; y++) { for(int x = 0; x < image->width; x++) { unsigned char color = (unsigned char)image->pixels[3 * (y * image->width + x)]; float h = height * ((color / 255.0f) - 0.5f); t->setHeight(x, y, h); } } delete image; t->computeNormals(); return t; }
이미지 파일에서 지형을 로드하는 기능은 다음과 같다.
1. 파일에서 비트 맵을 로드하기 위해 신뢰할 수 있는 ol'loadBMP 함수를 호출한다.
2. 배열의 픽셀을 살펴보고 이를 사용해 지형의 높이를 설정한다.
3. 0의 색은 - height / 2의 높이에 해당하며, 255의 색은 height / 2의 높이에 해당한다.
우리가 어떤 색 구성 요소를 사용하는지는 중요하지 않다. 특별한 이유없이 빨간색 구성 요소를 사용했다. 그런 다음 이미지를 삭제하고,
지형이 모든 법선을 계산하도록 한다.
이제 drawScene으로 넘어간다.
float scale = 5.0f / max(_terrain->width() - 1, _terrain->length() - 1); glScalef(scale, scale, scale); glTranslatef(-float(_terrain->width()) / 2, 0.0f, -float(_terrain->length()) / 2);
우리는 5개의 너비와 5개의 길이를 갖도록 지형을 확장한다. 그런 다음 중심으로 변환한다.
glColor3f(0.3f, 0.9f, 0.0f); for(int z = 0; z < _terrain->length() - 1; z++) { //Makes OpenGL draw a triangle at every three consecutive vertices glBegin(GL_TRIANGLE_STRIP); for(int x = 0; x < _terrain->width(); x++) { Vec3f normal = _terrain->getNormal(x, z); glNormal3f(normal[0], normal[1], normal[2]); glVertex3f(x, _terrain->getHeight(x, z), z); normal = _terrain->getNormal(x, z + 1); glNormal3f(normal[0], normal[1], normal[2]); glVertex3f(x, _terrain->getHeight(x, z + 1), z + 1); } glEnd(); }
여기에서 우리는 지형을 그린다. GL_TRIANGLE_STRIP은 새로운 기능이다. OpenGL은 사용자가 지정한 세 연속 점마다 삼각형을 그린다.
정점이 v1, v2, v3인 경우 OpenGL은 삼각형 (v1, v2, v3), (v2, v3, v4), (v3, v4, v5) 지형, 각 z에 대해 우리는 꼭지점 (0, h1, z), (0, h2, z + 1),
(1, h3, z), (1, h4, z + 1), (2, h5, z), (2, h6, z +1), ... 삼각형 스트립을 사용하는 것은 삼각형을 사용하는 것보다 편리할 뿐만 아니라,
그래픽 카드로 전송할 3D 정점 수가 적기 때문에 빠르다. 그래서 우리의 지형은 아래와 같이 그려진다:

우리가 지형을 그리는 방법은 x-z 격자의 각 셀을 대각선으로 오른쪽과 오른쪽을 사용해 두 개의 삼각형으로 조각한다.
우리는 각 셀을 조각하기 위해 다른 대각선을 사용할 수도 있었지만, 우리 지형이 "충분히 부드럽다"면 별로 중요하지 않다.
우리는 GL_QUADS를 대신 사용할 수도 있었지만 4개의 꼭지점이 같은 평면에 있지 않은 경우에는 그렇게 좋은 생각이 아니다.
int main(int argc, char** argv) { //... _terrain = loadTerrain("heightmap.bmp", 20); //... }
우리의 주요 기능에서는 loadTerrain을 호출해 3D 지형을 로드한다.
이제 돌아가서 우리가 우리의 법선을 어떻게 계산했는지 봅시다.
//Computes the normals, if they haven't been computed yet void computeNormals() { if (computedNormals) { return; } Vec3f** normals2 = new Vec3f*[l]; for(int i = 0; i < l; i++) { normals2[i] = new Vec3f[w]; } for(int z = 0; z < l; z++) { for(int x = 0; x < w; x++) { Vec3f sum(0.0f, 0.0f, 0.0f); Vec3f out; if (z > 0) { out = Vec3f(0.0f, hs[z - 1][x] - hs[z][x], -1.0f); } Vec3f in; if (z < l - 1) { in = Vec3f(0.0f, hs[z + 1][x] - hs[z][x], 1.0f); } Vec3f left; if (x > 0) { left = Vec3f(-1.0f, hs[z][x - 1] - hs[z][x], 0.0f); } Vec3f right; if (x < w - 1) { right = Vec3f(1.0f, hs[z][x + 1] - hs[z][x], 0.0f); } if (x > 0 && z > 0) { sum += out.cross(left).normalize(); } if (x > 0 && z < l - 1) { sum += left.cross(in).normalize(); } if (x < w - 1 && z < l - 1) { sum += in.cross(right).normalize(); } if (x < w - 1 && z > 0) { sum += right.cross(out).normalize(); } normals2[z][x] = sum; } }
먼저 근사 법선을 계산해 normals2 변수에 저장한다. 주어진 점에서 법선을 추정하는 한 가지 방법은 점에 정점이 있고, 그 옆에 두 점이 있는
삼각형에 수직인 벡터를 취하는 것이다. 예를 들어, 점의 꼭지점, 바로 오른쪽의 점 및 점에 대해 바깥 쪽의 점으로 삼각형을 가져올 수 있으며
그 점에 수직인 벡터를 취할 수 있다.
삼각형에 수직인 벡터를 찾으려면 두 개의 모서리의 교차곱을 취한다. 우리는 각 점에 대해 네 개의 가장자리를 in, out, left, right로 계산한다.
그런 다음 삼각형에 수직인 벡터를 결정하기 위해 한 쌍의 모서리의 교차 곱을 취한다. 점에 "인접한" 4개의 삼각형 각각에 대해 이를 수행하고
4개의 벡터의 평균을 취한다. (이는 합계에 비례한다)
기하학적으로 4개의 법선 벡터의 평균은 정확히 무엇인가? 이것은 법선을 근사하기 위해 생각한 것이다. 컴퓨터 그래픽의 기본 규칙은 옳은
것처럼 보이는 것이다. 그렇다면 이 이상한 평균화가 결국 효과가 있늕 ㅣ보자.
가장자리에 있는 점에 대해서는 if 문을 여러 개 사용해야 하는데, 인접한 삼각형이 4개 미만일 수 있기 때문이다.
좋아, 그래서 우리는 법선들을 계산했다. 그러나 각 법선이 인접한 법선과 더 비슷하도록 "부드럽게" 만드는 것이 좋다.
이렇게 하면 3D 장면의 조명이 더 부드럽게 보인다. 이것은 heightmap이 64개의 다른 높이만을 사용하기 때문에 특히 중요하다.
따라서 각 높이의 제한된 정밀도가 있어 조명이 거칠게 보인다. 우리에게 동기를 부여하기 위해, 여기에 우리의 장면을 부드럽지 않고
평활하게 한 법선과 나란히 비교해보겠다:
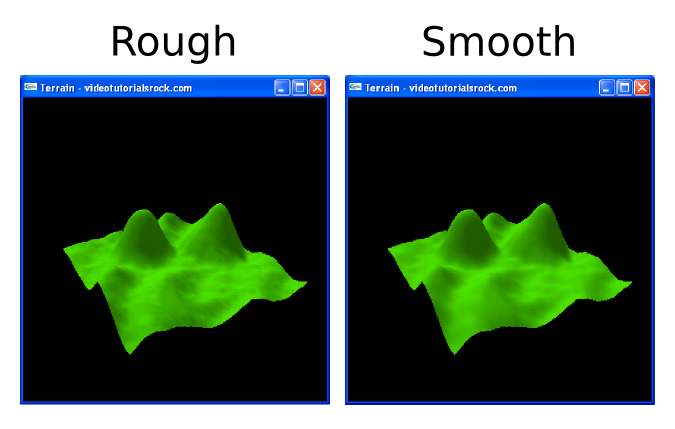
법선을 얼마나 부드럽게 할 것인가? 각각의 법선에 대해, 주변의 법선에 대해 평균을 구한다.
const float FALLOUT_RATIO = 0.5f; for(int z = 0; z < l; z++) { for(int x = 0; x < w; x++) { Vec3f sum = normals2[z][x]; if (x > 0) { sum += normals2[z][x - 1] * FALLOUT_RATIO; } if (x < w - 1) { sum += normals2[z][x + 1] * FALLOUT_RATIO; } if (z > 0) { sum += normals2[z - 1][x] * FALLOUT_RATIO; } if (z < 0) { sum += normals2[z + 1][x]; } if (sum.magnitude() == 0) { sum = Vec3f(0.0f, 1.0f, 0.0f); } normals[z][x] = sum; } }
따라서 각 법선 지점에서 "rough" 법선과 인접 점에서 "rough"법선의 가중 평균을 취한다. 각각의 인접한 법선은 0.5의 가중치를 가지며
그 지점의 법선은 1의 가중치를 가진다. 다시 말하면, 이 평균은 실제 의미가 없지만 여전히 장면을 좋게 만든다. 평균이 0 벡터로 판명되면
법선을 임의의 벡터로 설정한다. 이것은 정규화가 불가능하기 때문에 제로 벡터를 사용할 수 없기 때문이다. 그러나 우리는 무언가를 사용해야한다.
우리 장면의 조명은 꽤 좋아보인다. 이제 멋진 3D 지형을 만드는 방법을 알았다.
----------------------
----------------------
프로젝트에 진행하는 glm, glad 코드로 normal mapping shader를 사용해서 terrain을 구현했다.
height map을 어떻게 만드는지를 조사해야겠다.
'Game > Graphics' 카테고리의 다른 글
| OpenGL Figure draw function (2) | 2018.11.06 |
|---|---|
| Learn OpenGL - PBR : IBL(Specular IBL) (0) | 2018.10.21 |
| Learn OpenGL - PBR : IBL(Diffuse irradiance) (0) | 2018.10.20 |
| Learn OpenGL - PBR : Lighting (0) | 2018.10.20 |
| Learn OpenGL - PBR : Theory (0) | 2018.10.19 |



