link : https://learnopengl.com/PBR/Lighting
Lighting
이전 튜토리얼에서는 사실적인 물리적 기반 렌더러를 바닥에서 벗어나게하는 토대를 마련했다. 이 튜토리얼에서는 앞서 설명한 이론을
직접 (또는 분석) 광원을 사용하는 실제 렌더러로 변환하는데 초점을 맞춘다: point light, directional light, spotlights를 생각해라.
이전 튜토리얼의 최종 반사율 방정식을 다시 보고 시작하자:
이제 우리는 대부분 무슨 일이 벌어지고 있는지 알지만, 여전히 큰 불확실성은 장면의 전체 복사 강도 L을 얼마나 정확하게 나타낼 것인가이다.
이제 우리는 밝기 L (computer graphics land에서 해석 됨)이 주어진 입체각 ω에 대한 광원의 복사 에너지 또는 광 에너지를 측정한다는 것을
알고 있다. 우리의 경우에 우리는 입체각 ω가 무한히 작다고 가정했다. 이 경우 밝기는 단일 광선 또는 방향 벡터에 대해 광원의 flux를 측정한다.
이 지식을 감안할 때 이전 튜토리얼에서 축적한 조명 지식의 일부로 어떻게 변환할 수 있나? RGB 삼중항으로 변환된 (23.47, 21.31, 20.79)의
radiant flux(방사형플럭스)를 가진 단일 포인트 라이트가 있다고 상상해보아라. 이 광원의 radiant intensity(복사 강도)는 모든 나가는 방향 광선에서의
radiant flux(복사 유량)와 같다. 그러나, Ω에 걸쳐 모든 가능한 들어오는 빛 방향의 표면상의 특정 점 p를 음영처리 할 때, 단지 하나의 들어오는
방향 벡터 wi가 점 광원으로부터 직접 온다. 공간의 단일 지점에 있는 것으로 가정한 단일 광원만 있기 때문에 다른 모든 들어오는 빛 방향은
표면 지점에서 관찰된 0의 밝기를 가진다. p:
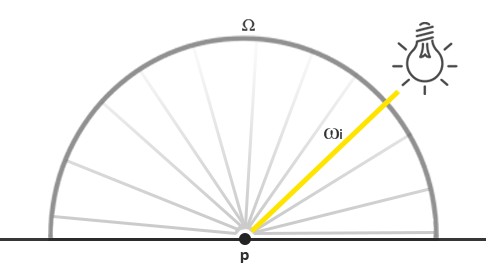
처음에는 광 감쇠가 점 광원에 영향을 미치지 않는다고 가정할 때, 입사 광선의 밝기는 빛의 위치에 관계없이 동일하다.
이것은 점 광이 우리가 보는 각도에 관계없이 동일한 복사 강도를 갖기 때문에 복사 빛의 강도로서 방사 강도를 효과적으로 모델링한다
: 상수 벡터(23.47, 21.31, 20.79)
그러나, 광도는 또한 입력으로서 위치 p를 취하고, 임의의 실제 점 광원은 광 감쇠를 고려하므로, 점 광원의 복사 강도는 점 p와 광원 사이의
거리 측정에 의해 결정된다. 그런 다음 원래의 방사 방정식에서 추출한대로 결과는 표면의 법선 벡터 n과 들어오는 빛의 방향 wi 사이의 내적에
의해 스케일된다.
좀 더 실제적인 용어로 표현하자면: direct point light의 경우 복사 휘도 함수 L은 p까지의 거리에 걸쳐 감쇠되고, n·wi로 스케일링된 빛의 색을
측정하지만, p를 치는 단일 광선에 대해서만 p의 빛의 방향 벡터와 같다. 코드에서 이것은 다음으로 변환된다:
vec3 lightColor = vec3(23.47, 21.31, 20.79);
vec3 wi = normalize(lightPos - fragPos);
float cosTheta = max(dot(N, Wi), 0.0);
float attenuation = calculateAttenuation(fragPos, lightPos);
float radiance = lightColor * attenuation * cosTheta;다른 용어를 제외하고 이 코드는 당신에게 익숙 할 것이다: 이것은 우리가 지금까지 조명을 퍼뜨리고 있었던 방식이다.
직사광선에 관해서는 빛의 방향 벡터가 단지 표면의 광도에 기여하기 때문에 조명을 계산한 것과 비슷하게 광도가 계산된다.
단일 지점에서 발생하는 다른 유형의 광원에 대해서도 우리는 비슷하게 빛을 계산한다. 예를 들어, directional light는 감쇠 계수가 없는
상수 wi를 가지며, spotlight는 일정한 복사 강도를 갖지 않지만 spotlight의 순방향 벡터에 의해 스케일링되는 것은 일정한 방사 강도를
가질 것이다.
이것은 또한 우리를 표면의 반구 Ω에 대한 적분 ∫으로 되돌아가게한다. 단일 표면 점을 음영 처리하는동안 모든 기여 광원의 단일 위치를
미리 알기 때문에 통합을 시도하고 해결할 필요가 없다. 각 광원이 표면의 밝기에 영향을 미치는 단 하나의 빛의 방향만을 가지고 있다면
(알려진) 광원 수를 직접 취해 총 방사 조도를 계산할 수 있다. 이로 인해 direct light에 대한 PBR은 상대적으로 간단해진다. 왜냐하면 우리가
효과적으로 기여하는 광원을 반복해야하기 때문이다. 나중에 IBL 튜토리얼에서 환경 조명을 고려할 때 어떤 방향에서든 빛이 올 수 있기 때문에
필수 요소를 고려해야한다.
A PBR surface model
앞서 설명한 PBR 모델을 구현하는 조각 쉐이더를 작성해 보겠다. 먼저 표면을 음영 처리하는데 필요한 관련 PBR 입력을 받아야한다:
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;
uniform vec3 camPos;
uniform vec3 albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;우리는 일반 정점 쉐이더와 객체의 표면에 대한 일정한 material property 세트로부터 계산된 표준 입력을 가져온다.
그런 다음 조각 쉐이더가 시작될 때 조명 알고리즘에 필요한 일반적인 계산을 수행한다: the surface:
void main()
{
vec3 N = normalize(Normal);
vec3 V = normalize(camPos - WorldPos);
[...]
}Direct lighting
이 튜토리얼의 예제 데모에서는 장면의 방사 조도를 직접 나타내는 총 4개의 점등이 있다. 반사율 방정식을 충족시키기 위해 각 광원에 대해
반복하고, 개별 광도를 계산하고 BRDF 및 광의 입사각으로 조정된 기여도를 합계한다. 우리는 direct 광원에 대해 ∫ over Ω의 적분을
푸는 것으로 루프를 생각할 수 있다. 첫째, light 변수를 계산한다:
vec3 Lo = vec3(0.0);
for(int i = 0; i < 4; ++i)
{
vec3 L = normalize(lightPositions[i] - WorldPos);
vec3 H = normalize(V + L);
float distance = length(lightPositions[i] - WorldPos);
float attenuation = 1.0 / (distance * distance);
vec3 radiance = lightColors[i] * attenuation;
[...] 우리가 선형 공간에서 조명을 계산할 때 우리는 보다 물리적으로 올바른 역 제곱법칙으로 감쇠시킨다.
그런 다음 각 조명에 대해 전체 Cook-Torrance 반사 BRDF 용어를 계산하려고 한다:
우리가 하고 싶은 첫 번째 일은 정반사와 확산 반사 사이의 비율을 계산하는 것이다. 표면이 빛을 반사하는 정도와 빛을 굴절시키는 정도를
계산하는 것이다. 이전 튜토리얼에서 fresnel 방정식은 다음과 같이 계산한다:
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
} Fresnel-Schlick 근사법은 제로 방병률에서 표면 반사로 알려진 F0 파라미터 또는 표면에서 직접 볼 때 표면이 얼마나 많이 반사하는지를
예상한다. F0는 소재마다 다르며 대형 소재 데이터베이스에서처럼 금속에 착색된다. PBR 케탈 워크 플로우에서 우리는 대부분의 유전체
표면이 알베도 값에 의해 주어진 것처럼 금속 표면에 대해 F0를 지정하는동안 상수 F0가 0.04로 시각적으로 올바른 것으로 가정한다.
이것은 다음과 같이 코드로 변환된다:
vec3 F0 = vec3(0.04);
F0 = mix(F0, albedo, metallic);
vec3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);알 수 있듯이 비금속 표면의 경우 F0는 항상 0.04이지만 금속 속성이 주어지면 원본 F0와 알베도 값을 선형적으로 보간해 곡면의 금속성을
기준으로 F0를 변경한다.
주어진 F에서 나머지 계산 항은 정규 분포 함수 D와 기하학 함수 G이다.
직접적인 PBR 조명 쉐이더에서 해당 코드는 다음과 같다:
float DistributionGGX(vec3 N, vec3 H, float roughness)
{
float a = roughness*roughness;
float a2 = a*a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH*NdotH;
float num = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return num / denom;
}
float GeometrySchlickGGX(float NdotV, float roughness)
{
float r = (roughness + 1.0);
float k = (r*r) / 8.0;
float num = NdotV;
float denom = NdotV * (1.0 - k) + k;
return num / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx2 = GeometrySchlickGGX(NdotV, roughness);
float ggx1 = GeometrySchlickGGX(NdotL, roughness);
return ggx1 * ggx2;
}여기서 중요한 점은 이론 튜토리얼과 달리 거칠기 매개 변수를 이러한 함수에 직접 전달한다는 것이다. 이 방법으로 원래의 거칠기 값에
대해 몇가지 용어를 수정할 수 있다. 디즈니가 관찰하고 Epic Games에서 채택한 관찰 결과에 따르면 조명은 기하학 및 정규 분포 함수의
거칠기를 보다 정확하게 보정하다.
두 함수를 모두 정의한 경우 반사율 루프에서 NDF와 G항을 계산하는 것은 간단하다:
float NDF = DistributionGGX(N, H, roughness);
float G = GeometrySmith(N, V, L, roughness); 이렇게 하면 Cook-Torrance BRDF를 계산할 수 있다:
vec3 numerator = NDF * G * F;
float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0);
vec3 specular = numerator / max(denominator, 0.001); 어떤 내적이 0.0으로 끝나는 경우 0으로 나누는 것을 막기 위해 분모를 0.001로 제한한다.
이제 반사율 방정식에 대한 각 광원의 기여도를 마침내 계산할 수 있다. fresnel 값이 kS에 직접적으로 대응하므로 F를 사용해 표면에 닿는 빛의
반사를 나타낼 수 있다. kS에서 우리는 다음 굴절률 kD를 직접 계산할 수 있다:
vec3 kS = F;
vec3 kD = vec3(1.0) - kS;
kD *= 1.0 - metallic; kS가 반사되는 빛의 에너지를 나타내는 것으로 보는 것, 빛의 에너지의 나머지 비율은 우리가 kD로 저장하는 굴절된 빛이다.
또한, 금속 표면은 빛을 굴절시키지 않으므로 확산 반사가 없기 때문에 표면이 금속인 경우 kD를 무효화해 이 특성을 강화한다.
이것은 각 빛의 나가는 반사율 값을 계산하는데 필요한 최종 데이터를 준다:
const float PI = 3.14159265359;
float NdotL = max(dot(N, L), 0.0);
Lo += (kD * albedo / PI + specular) * radiance * NdotL;
}결과로 나온 Lo 값 또는 나가는 광도는 반사율 방정식의 적분 ∫ over Ω의 결과이다. 우리는 조각에 영향을 줄 수 있는 4개의 들어오는 빛의
방향을 정확히 알기 때문에 가능한 모든 들어오는 빛의 방향에 대한 적분을 실제로 풀지 않아도 된다. 이 덕분에 들어오는 빛 방향을 현장의
조명 수에 직접 연결할 수 있다.
왼쪽은 직접 조명 결과 Lo에 (즉흥적인) ambient 항을 추가하는 것이다. 그리고 우리는 조각의 최종 조명된 색을 갖는다:
vec3 ambient = vec3(0.03) * albedo * ao;
vec3 color = ambient + Lo; Linear and HDR rendering
지금까지 우리는 모든 계산이 선형 색 공간에 있다고 가정했으며 이를 위해 쉐이더의 끝에서 감마 보정을 해야한다. 선형 공간에서의 조명 계산은
PBR이 모든 입력을 선형으로 요구하기 때문에 엄청나게 중요하다. 이것을 고려하지 않으면 잘못된 조명이 된다. 또한, 빛의 입력 값을 물리적 등가물에
가깝게해 빛의 휘도 또는 색상 값이 높은 값의 스펙트럼에서 크게 달라질 수 있도록 한다. 결과적으로 Lo는 매우 빠르게 증가해 기본 저동적범위(LDR)
출력으로 인해 0.0과 1.0사이에서 클램핑된다. 우리는 감마 수정 전에 Lo와 톤 또는 노출을 HDR(High Dynamic Range)값을 LDR에 올바르게 맵핑해
이 문제를 해결한다:
color = color / (color + vec3(1.0));
color = pow(color, vec3(1.0/2.2)); 여기서 우리는 Reinhard 연산자를 사용해 HDR 색상을 톤 맵핑하고, 아마도 매우 다양한 복사 조도의 높은 동적 범위를 보존 한 후에
색상을 감마 보정한다. 별도의 프레임 버퍼 또는 후 처리 단계가 없으므로 톤 맵핑 단계와 감마 보정 단계를 직접 앞으로 조각 쉐이더의 끝에
적용 할 수 있다.

선형 색상 공간과 높은 동적 범위를 모두 고려하는 것은 PBR 파이프 라인에서 매우 중요하다. 이 기능이 없으면 빛의 강도가 다양하고
높거나 낮은 세부 사항을 제대로 포착 할 수 없으며 계산이 잘못되어 시각적으로 불쾌해진다.
Full direct lighting PBR shader
이제 남아있는 모든 것은 조각 쉐이더의 출력 채널에 최종 톤 맵핑 및 감마 보정된 색상을 전달하는 것이며 직접 PBR 조명 쉐이더를 사용한다.
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;
// material parameters
uniform vec3 albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;
// lights
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];
uniform vec3 camPos;
const float PI = 3.14159265359;
float DistributionGGX(vec3 N, vec3 H, float roughness);
float GeometrySchlickGGX(float NdotV, float roughness);
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness);
void main()
{
vec3 N = normalize(Normal);
vec3 V = normalize(camPos - WorldPos);
vec3 F0 = vec3(0.04);
F0 = mix(F0, albedo, metallic);
// reflectance equation
vec3 Lo = vec3(0.0);
for(int i = 0; i < 4; ++i)
{
// calculate per-light radiance
vec3 L = normalize(lightPositions[i] - WorldPos);
vec3 H = normalize(V + L);
float distance = length(lightPositions[i] - WorldPos);
float attenuation = 1.0 / (distance * distance);
vec3 radiance = lightColors[i] * attenuation;
// cook-torrance brdf
float NDF = DistributionGGX(N, H, roughness);
float G = GeometrySmith(N, V, L, roughness);
vec3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);
vec3 kS = F;
vec3 kD = vec3(1.0) - kS;
kD *= 1.0 - metallic;
vec3 numerator = NDF * G * F;
float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0);
vec3 specular = numerator / max(denominator, 0.001);
// add to outgoing radiance Lo
float NdotL = max(dot(N, L), 0.0);
Lo += (kD * albedo / PI + specular) * radiance * NdotL;
}
vec3 ambient = vec3(0.03) * albedo * ao;
vec3 color = ambient + Lo;
color = color / (color + vec3(1.0));
color = pow(color, vec3(1.0/2.2));
FragColor = vec4(color, 1.0);
} 이전 튜토리얼의 이론과 반사율 방정식에 대한 지식으로 이 쉐이더는 더 이상 위압적이지 않아야한다. 우리가 이 쉐이더, 4포인트 라이트와
꽤 많은 수의 스페어를 가지고 수직과 수평 축에서 각각 금속성과 조도 값을 바꾼다면 다음과 같은 것을 얻을 수 있다:

아래에서 위로 금속 값의 범위는 0.0에서 1.0이며, 거칠기는 왼쪽에서 오른쪽으로 0.0에서 1.0까지 증가한다. 이 두가지 매개 변수를
변경하는 것만으로 다양한 재료를 이미 표시할 수 있다.
Textured PBR
이제 시스템이 균일한 값 대신 텍스처로 표면 매개 변수를 받아들이도록 함으로써 표면 재질의 특성을 조각 단위로 제어할 수 있다:
[...]
uniform sampler2D albedoMap;
uniform sampler2D normalMap;
uniform sampler2D metallicMap;
uniform sampler2D roughnessMap;
uniform sampler2D aoMap;
void main()
{
vec3 albedo = pow(texture(albedoMap, TexCoords).rgb, 2.2);
vec3 normal = getNormalFromNormalMap();
float metallic = texture(metallicMap, TexCoords).r;
float roughness = texture(roughnessMap, TexCoords).r;
float ao = texture(aoMap, TexCoords).r;
[...]
}아티스트의 알베도 텍스처는 일반적으로 sRGB 공간에서 작성되므로 조명 계산에서 알베도를 사용하기 전에 선형 공간으로 변환해야한다.
ambient occlusion map을 생성하는 시스템 아티스트를 기반으로 sRGB에서 선형 공간으로 변환해야 할 수도 있따. 금속 및 조도 맵은
거의 항상 선형 공간에서 작성된다.
이전 구의 재질 속성을 텍스처로 바꾸면 이전에 사용한 조명 알고리즘보다 크게 개선되었다:

금속 표면은 확산 반사율이 없기 때문에 direct light 환경에서는 너무 어둡게 보인다. 다음 튜토리얼에서 초점을 맞추고 있는 환경의 반사 조명을
고려하면 더 정확하게 보인다.
아직 PBR 렌더링 데모 중 일부가 시각적으로 인상적이지는 않지만 이미지 기반 조명이 내장되어 있지 않으므로 우리 시스템은 여전히 물리적
기반 렌더러이며 IBL이 없어도 볼 수 있다. 조명이 훨씬 사실적으로 보인다.
'Game > Graphics' 카테고리의 다른 글
| Learn OpenGL - PBR : IBL(Specular IBL) (0) | 2018.10.21 |
|---|---|
| Learn OpenGL - PBR : IBL(Diffuse irradiance) (0) | 2018.10.20 |
| Learn OpenGL - PBR : Theory (0) | 2018.10.19 |
| Learn OpenGL - Advanced Lighting : SSAO (0) | 2018.10.11 |
| Learn OpenGL - Advanced Lighting : Deferred Shading (0) | 2018.10.07 |





