link : https://learnopengl.com/PBR/Theory
Theory
PBR, 또는 더 일반적으로 physically based rendering으로 알려진 렌더링 기술의 집합은 물리적인 세계의 것과 더 가깝게 일치하는
동일한 기본 이론에 기반한다. 물리적 기반 렌더링은 물리적으로 그럴듯한 방법으로 비을 모방하는 것을 목표로 하기 때문에
Phong 및 Blinn-Phong과 같은 원래의 조명 알고리즘과 비교할 때 일반적으로 더 현실적으로 보인다.
실제 물리학에 매우 가깝기 때문에 우리는 물리적인 매개 변수를 기반으로 표면 재질을 제작 할 수 있다. 조명을 돋보이게 하기
위해 값싼 해킹과 개조 작업을 하지 않아도된다. 물리적 매개 변수에 기반한 저작물의 더 큰 장점 중 하나는 조명 조건에 관계없이
이러한 자료가 올바르게 표시된다는 것이다. 비 PBR 파이프 라인에서는 그렇지 못하다.
그럼에도 불구하고 실제 기반 렌더링은 현실의 근사치이므로 physical shading이 아니라 physically based shading이라고 한다.
물리적 기반으로 간주되는 PBR 조명 모델의 경우 다음 3가지 조건을 충족해야한다.
1. microfacet 표면 모델을 기반으로 해라
2. 에너지를 보존해라
3. 물리적 기반 BRDF를 사용해라
이 PBR 튜토리얼 시리즈/가이드에서 우리는 원래 Disney가 탐구한 PBR 접근 방식에 초점을 맞추고 Epic Games의 실시간 디스플레이에
채택했다. Metallic workflow를 기반으로 하는 그들의 접근법은 문서화되어 널리 사용되는 엔진에서 채택되어 시각적으로 놀라운 것처럼
보인다. 시리즈가 끝날 무렵 우리는 다음과 같은 모습을 보일 것이다:

이 튜토리얼 시리즈의 항목은 다소 고급이므로 OpenGL 및 shading lighting을 잘 이해하는 것이 좋다. 이 시리즈에 필요한 고급 지식에는
프레임 버퍼, 큐브 맵, 감마 보정, HDR 및 normal mapping이 있다. 우리는 또한 일부 고급 수학을 탐구 할 것이지만 가능한 명확하게 개념을
설명하기 위해 최선을 다할 것이다.
The microfacet model
모든 PBR 기술은 microfacets 이론을 기반으로 한다. 이 이론은 마이크로 스케일이라 불리는 어떤 표면이라도 마이크로피트라 불리는
작은 반사 거울로 설명 될 수 있다고 설명한다. 표면 거칠기에 따르면 이러한 작은 거울의 정렬은 상당히 다를 수 있다:

표면이 거칠수록 각 미세 협곡이 표면을 따라 더 복잡하게 배열된다. 이러한 미세한 거울 정렬의 효과는 반사조명/반사에 대해 구체적으로
이야기 할 때 들어오는 광선이 더 거친 표면에서 완전히 다른 방향으로 산란할 확률이 높아지고 결과적으로 더 넓은 반사가 발생한다는 것이다.
대조적으로, 매끄러운 표면에서 광선은 대략 동일한 방향으로 반사하는 경향이 있어 보다 작고 선명한 반사를 제공한다.

미세한 수준에서는 표면이 완전히 매끄럽지 않지만 이러한 미세 기둥은 픽셀 단위로 구별 할 수 없을만큼 작기 때문에 거칠기 매개 변수를
고려할 때 표면의 미세 조도 거칠기를 통계적으로 근사하다. 표면의 거칠기를 기반으로 우리는 대략적으로 어떤 벡터 h에 정렬된 마이크로 벽의
비율을 계산할 수 있다. 이 벡터 h는 빛 I와 뷰 v 벡터 사이의 중간에 위치하는 중간 벡터이다. 우리는 앞서 조명 튜토리얼에서 I와 v의 합으로
길이를 나눈 값으로 계산된 중간 벡터를 논의했다:
마이크로 안테나가 중간 벡터에 정렬될수록 거울 반사가 날카롭고 강해진다. 0과 1사이에서 변화하는 조도 매개 변수와 함께 우리는
마이크로 패싯의 정렬을 통계적으로 근사 할 수 있다:

더 높은 거칠기 값은 보다 매끄러운 표면의 더 작고 더 선명한 반사 모양과 달리 훨씬 더 큰 반사 모양을 만든다.
Energy conservation
microfacet 근사법은 일종의 에너지 보존 방식을 사용한다. 나가는 빛 에너지는 들어오는 빛 에너지를 초과해서는 안된다. (방출면 제외)
위 이미지를 보면 정반사 영역이 증가하지만 거칠기가 증가하면 밝기가 감소하는 것을 볼 수 있다. specular 모양의 크기에 관계없이
specular intensity가 각 픽셀에서 같으면 거친 표면은 훨씬 많은 에너지를 방출해 에너지 보존 원칙을 위배하게 된다.
이러한 이유로 우리는 매끄러운 표면에서 더 강하게 반사되는 반사광을 볼 수 있으며 거친 표면에서는 더 희미하게 보인다.
에너지 보존을 위해 우리는 확산 빛과 반사 광선을 명확하게 구별해야한다. 광선이 표면에 부딪치는 순간 굴절 부분과 반사 부분 모두에서
분할된다. 반사 부분은 직접 반사되어 표면에 들어가지 않는 빛이다. 이것은 우리가 반사 조명으로 알고 있는 것이다. 굴절 부분은 표면에
들어가서 흡수된 나머지 빛이다. 이것은 우리가 확산 조명으로 알고 있는 것이다.
굴절된 빛이 표면에 닿아 즉시 흡수되지 않기 때문에 여기에 약간의 뉘앙스가 있다. 물리학에서 우리는 빛이 모든 에너지를 잃을 때까지
계속 전진하는 에너지 빔으로 간주 될 수 있음을 안다. 광선이 에너지를 잃는 방법은 충돌에 의한 것이다. 각 재료는 아래 그림과 같이
광선과 충돌 할 수 있는 작은 입자로 구성된다. 입자는 각 충돌시 빛의 에너지 일부 또는 전부를 흡수해 열로 변환된다.
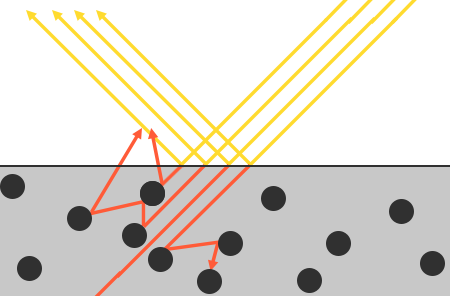
일반적으로 모든 에너지가 흡수되는 것은 아니며 빛은 에너지가 고갈되거나 표면에서 다시 빠져 나올때까지 다른 입자와 충돌하는
임의의 방향으로 산란을 계속한다. 표면에서 재 방출되는 광선은 표면에서 관찰되는 색상에 영향을 준다. 물리적으로 렌더링 할 때
우리는 모든 굴절된 빛이 매우 작은 영역의 충격에서 흡수되고 흩어지면서 거리에서 표면을 빠져 나온 흩어져있는 광선의 영향을 무시한다는
단순한 가정을 한다. 이를 고려한 특정 쉐이더 기술은 피부, 대리석, 왁스와 같은 재질의 시각적 품질을 크게 개선하지만 성능면에서
가격이 저렴하다.
반사와 굴절에 관해서 미묘한 점은 금속성 표면이다. 금속 표면은 비금속 표면에 비해 빛에 대해 다르게 반응한다. 금속 표면은 동일한
반사 및 굴절 원리를 따르지만 모든 굴절된 빛은 산란없이 직접 흡수되어 reflected or specular light만을 남긴다. 금속 표면은 확산되는 색상을
보이지 않는다. 금속과 비금속 표면 사이의 이러한 명백한 구별 때문에 그들은 PBR 파이프 라인에서 다르게 취급된다.
우리는 이 기사에 대해 더 자세히 다루겠다.
반사광과 굴절된 빛의 차이는 에너지 보존과 관련해 또 다른 관찰로 이어진다. 어떤 빛 에너지가 반사되더라도 더 이상 물질 자체에 흡수되지
않는다. 따라서, 굴절된 빛으로 표면에 들어가기 위해 남겨진 에너지는 우리가 반사를 고려한 결과 직접 에너지이다.
우리는 들어오는 광선이 에너지를 반영해 백분율을 나타내는 정사각형 부분을 먼저 계산함으로써 이 에너지 보존 관계를 보존한다.
굴절된 빛의 분율은 다음과 같이 거울 반사율 부분에서 직접 계산된다:
float kS = calculateSpecularComponent(...); // reflection/specular fraction
float kD = 1.0 - kS; // refraction/diffuse fraction이렇게하면 에너지 보존 원칙을 준수하면서 들어오는 빛이 반사하는 양과 굴절하는 양을 알 수 있다.
이 접근법을 감안할 때 굴절/호가산 및 반사/정반사 기여가 모두 1.0을 초과하는 것은 불가능하며, 따라서 자신의 에너지 합계가 들어오는
빛 에너지를 초과하지 않도록 보장한다. 이전의 조명 튜토리얼에서는 고려하지 않은 것이다.
The reflectance equation
이것은 렌더링 방정식이라고 불리는 것에 우리를 데려온다. 정교한 방정식은 아주 똑똑한 사람들이 만들었으며 현재 그것은
빛의 시각을 시뮬레이션 하기 위한 최고의 모델이다. 물리적 기반 렌더링은 반사 방정식으로 알려진 렌더링 방정식보다 특수화된
버전을 강하게 따른다. PBR을 제대로 이해하려면 먼저 반사율 방정식을 확실하게 이해하는 것이 중요하다:
반사율 방정식은 처음에 힘들게 보인다. 그러나 천천히 해부하면 천천히 시작된다는 것을 알게 될 것이다. 방정식을 이해하기 위해,
우리는 약간의 방사선 측정을 탐구해야한다. 방사선 측정은 전자기 방사선(가시 광선 포함)의 측정이다. 표면과 방향에 대해 빛을 측정하는데
사용할 수 있는 여러 가지 방사량이 있지만 여기서는 L로 표시된 방사율로 알려진 반사율 방정식과 관련이 있는 단일 방사형만 논의한다.
방사형은 빛의 크기 또는 강도를 계량하는데 사용된다. 먼저 밝기는 여러 물리량의 조합이므로 먼저 이해해야할 사항이 있다.
Radiant flux : 복사 광속 Φ는 와트 단위로 측정된 광원의 전송 에너지이다. 빛은 여러 파장의 에너지를 총체적으로 합한 것이다.
각 파장은 특정 색상과 관련된다. 따라서 광원의 방출 에너지는 모든 다른 파장의 함수로 생각할 수 있다. 390nm 내지 700nm 사이의 파장은
가시광 스펙트럼, 즉 인간의 눈이 인지 할 수 있는 파장의 일부로 간주된다. 아래는 일광의 파장당 다른 에너지의 이미지이다:
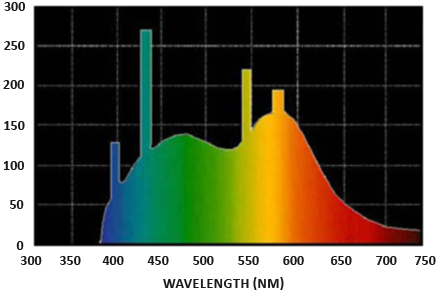
복사 광속은 다른 파장의 이 기능의 총 면적을 측정한다. 이 파장의 측정 값을 컴퓨터 그래픽의 입력으로 직접 사용하는 것은 약간 실용적이지
않으므로 다양한 파장 강도의 함수가 아닌 방사 플럭스를 단순화하는 대신 RGB로 인코딩된 밝은 색상의 삼중항으로 사용한다.
(또는 우리가 흔히 말하는 : 밝은 색) 이 인코딩은 정보의 손실로 이어지지만 일반적으로 시각적 측면에서 무시할 수 있다.
Solid angle : ω로 표시된 입체각은 단위 구상에 투영된 모양의 크기 또는 면적을 나타낸다. 이 단위 구상에 투영된 모양의 영역을 입체각이라 한다.
볼륨의 방향으로 입체각을 시각화할 수 있다:
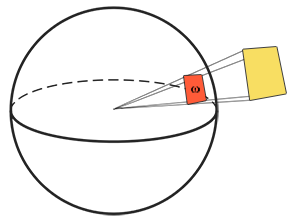
이 단위 구의 중심에 있는 관찰자가 되어 모양의 방향을 보고 생각해보아라. 실루엣의 크기는 입체각이다.
Radiant intensity : 복사 강도는 입체각당 복사 광량 또는 투영된 영역에 대한 광원의 강도를 단위 구에 대해 측정한다.
예를 들어 전 방향으로 똑같이 방출되는 무 지향성 빛이 주어지면 복사 강도는 특정 영역에 걸쳐 우리에게 에너지를 줄 수 있다.
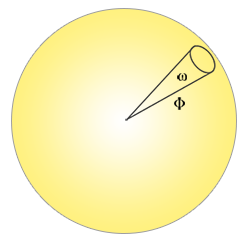
복사 강도를 나타내는 방정식은 다음과 같이 정의된다:
여기서 I는 입체각 ω에 대한 방사광 Φ이다.
복사 광속, 복사 강도 및 입체각에 대한 지식으로 우리는 복사 강도 Φ의 빛의 입체각 ω에 대해 영역 A에 대한 총 관측 에너지로 설명되는
복사 강도 방정식을 최종적으로 설명할 수 있다.
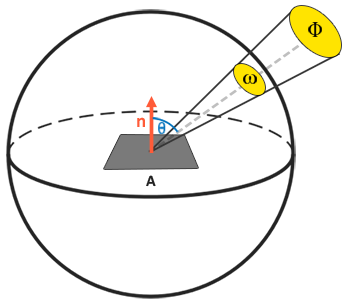
Radiance는 표면의 법선에 대한 빛의 입사각 θ에 의해 스케일된 영역의 빛의 양을 방사 측정한다.
cosθ : 빛은 표면에 직접 방사되는 양이 적으면 적을수록 약하고, 직접적으로는 강한 표면에 수직이다.
이는 cosθ가 광원의 방향 벡터와 표면의 법선 사이의 내적(dot product)과 직접적으로 일치하므로 기본 조명 튜토리얼에서 확산 조명에 대한
인식과 유사하다:
float cosTheta = dot(lightDir, N); 우리 관심의 대상인 대부분이 물리량으로 구성되어 있기 때문에 방사도 방정식은 매우 유용하다. 입체각 ω와 면적 A가 무한히 작다고 가정하면,
공간의 단일 지점을 타격하는 단일 광선의 광속을 측정하기 위해 빛을 사용할 수 있다. 이 관계는 단일 점에 영향을 미치는 단일 광선의 복사
강도를 계산할 수 있게 해준다. 우리는 입체각 ω를 방향 벡터 ω로, 그리고 A를 점 p로 효과적으로 변환한다. 이 방법으로 쉐이더에서 직접 빛을
사용해 단일 광선의 조각당 기여도를 계산할 수 있다.
실제로, 우리가 일반적으로 광도에 관해서는 우리는 모든 irradiance로 알려진 모든 광도의 합인 점 p로 들어오는 빛을 돌본다.
광도와 복사 조도를 알고 있으면 반사율 방정식으로 되돌아 갈 수 있다.
렌더링 방정식에서의 L은 어떤 점 p의 광도와 들어오는 방향 벡터 ωi로 생각할 수 있는 무한히 작은 입체각 ωi의 일부를 나타낸다.
cosθ는 반사율 방정식에서 n⋅ωi로 나타내는 표면에 대한 빛의 입사각에 기초해 에너지를 스케일링한다는 것을 기억해라.
반사율 방정식은 관측자로 나가는 방향인 방향 ωo에서 점 p의 반사 휘도 Lo (p, ωo)의 합을 계산한다.
또는 다르게 표현하면: Lo는 ωo에서 보았을 때 점 p에 대한 광원의 복사 조도의 반사된 합계를 측정한다.
반사율 방정식은 모든 입사 빛이 합계인 조사량을 기반으로 하기 때문에 우리는 단 하나의 들어오는 빛의 방향뿐만 아니라 점 p를 중심으로
하는 반구 Ω 내의 모든 들어오는 빛의 방향의 빛을 측정한다. 반구는 표면의 정상 n 주위에 정렬된 반구라고 표현할 수 있다:
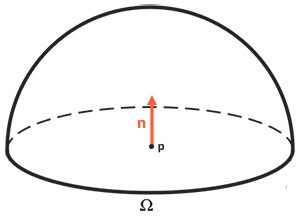
영역 내부의 값 합계를 계산하기 위해 반구 Ω 내의 모든 들어오는 방향 dωi에 대해 반사율 방정식에 ∫으로 표시된 적분이라는 수학적 구조를
사용한다. 적분은 함수 영역을 분석적 또는 수치적으로 계산할 수 있다. 렌더링과 반사 방정식 모두에 대한 분석적인 해가 없기 때문에
수치적으로 이산적으로 풀기를 원할 것이다. 이것은 반구 Ω에 대한 반사 방정식의 작은 이산 단계의 결과를 취하고 단게 크기에
대한 결과의 평균을 의미한다. 이것은 리만 합(Riemann Sum)으로 알려져 있으며 대략 다음과 같이 코드에서 시각화 할 수 있다:
int steps = 100;
float sum = 0.0f;
vec3 P = ...;
vec3 Wo = ...;
vec3 N = ...;
float dW = 1.0f / steps;
for(int i = 0; i < steps; ++i)
{
vec3 Wi = getNextIncomingLightDir(i);
sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW;
}dW로 단계를 스케일링하면 합계는 적분 함수의 총 면적 또는 부피와 같다. 각각의 이산 단계를 측정하기위한 dW는 반사 방정식에서
dωi로 생각할 수 있다. 수학적으로 dωi는 우리가 적분을 계산하는 연속적인 기호이며 코드에서 dW와 직접적으로 관련이 없는 반면
이 방식으로 생각하는데 도움이 된다. 이산 단계를 사용하면 함수의 총 면적을 대략적으로 알 수 있다. 주의깊은 독자는 단계 수를 늘림으로써
Riemann Sum의 정확도를 높일 수 있음을 알 수 있다.
반사율 방정식은 반경 ρ에 의해 스케일된 반경 ρ에 대한 모든 입사광 방향 ωi의 방사율을 합산해 뷰어의 방향으로 반사광의 총합을 반환한다.
우리가 IBL 튜토리얼에서 논의 할 모든 입사 방향의 밝기를 측정하는 환경 맵에 익숙하거나 익숙한 환경에서 빛이 들어올 수 있다.
이제 유일하게 알려지지 않은 왼쪽은 BRDF 또는 양방향 반사 분포 함수로 알려진 fr 기호이다. 이 기호는 표면의 재료 특성을 기반으로
들어오는 방사를 조정하거나 무게를 재어준다.
BRDF
BRDF 또는 Bidirectional reflective distribution function(양방향 반사 분포 함수)는 입력 (빛) 방향 ωi, 나가는 (뷰) 방향 ωo, 표면 법선 n 및
microsurface의 거칠기를 나타내는 표면 파라미터 a를 입력으로 받는 함수이다. BRDF는 물질 특성을 고려할 때 불투명 표면의 최종 반사광에
각 개별 광선이 얼마나 많이 기여하는지 대략적으로 나타낸다. 예를 들어, 표면이 완벽하게 매끄러운 표면(거울처럼)을 가지고 있다면
BRDF 함수는 함수는 모든 들어오는 광선 ωi에 대해 0.0을 반환한다. 나가는 광선 ωo는 1.0을 반환한다.
BRDF는 이전에 논의된 microfacet 이론을 기반으로 소재의 반사 및 굴절 특성을 근사한다. BRDF가 물리적으로 그럴듯하게 보이기 위해서는
에너지 보존 법칙을 존중해야한다. 즉, 반사광의 합이 들어오는 빛의 양을 초과해서는 안된다. 기술적으로 Blinn-phong은 동일한 ωi와 ωo를
입력으로 사용하는 BRDF로 간주된다. 그러나 Blinn-phong은 에너지 보존 원칙을 준수하지 않으므로 물리적 기반으로 간주되지 않는다.
표면의 빛에 대한 반응을 대략적으로 나타내기 위해 몇 가지 물리적 기반 BRDF가 있다. 그러나 거의 모든 실시간 렌더링 파이프 라인은
Cook-Torrance BRDF라고하는 BRDF를 사용한다.
Cook-Torrance BRDF는 확산 및 반사 부분을 모두 포함한다:
여기에서 kd는 ks가 반사되는 비율로 굴절되는 유입광 에너지의 앞서 언급한 비율이다. BRDF의 왼쪽에는 flamebert로 표시된 방정식의
확산 부분이 나와있다. 이것은 Lambertian diffuse로 알려져있다. Diffuse shading에 사용된 것과 유사하다. 이 쉐이딩은 다음과 같이 나타나는
상수 요소이다:
c는 albedo 또는 표면 컬러이다. pi에 의한 나누기는 BRDF가 포함된 이전에 표시된 적분이 π로 스케일링되기 때문에 확산 광을 표준화하기 위해
존재한다.
BRDF의 확산 부분에 대한 다른 방정식이 존재하는데, 이는 보다 사실적으로 보일 수 있지만 계산상 비싸다.
그러나 에픽 게임스(Epic Games)에 의해 결론 지으면서, Lambertian diffuse의 대부분은 실시간 렌더링 목적에 충분하다.
BRDF의 반사 부분은 좀 더 고급적이며 다음과 같이 설명된다:
Cook-Torrance 반사 BRDF는 세 개의 함수와 분모의 정규화 인수로 구성된다. D, F, G 기호 각각은 표면의 반사 특성의 특정 부분을
근사하는 함수 유형을 나타낸다. 이들은 정규분포함수, Fresnel 방정식, 기하학 함수로 정의된다.
- Normal distribution function : 표면의 micropacets이 표면의 거칠기의 영향을 받는 중간 벡터에 정렬되는 양을 근사한다.
이것이 microfacets을 근사하는 주요 함수이다.
- Geometry function : microfacets의 자체 음영 속성을 설명한다. 표면이 상대적으로 거칠면 표면의 미세 기둥이 다른 미세 기둥을
가릴 수 있어서 표면이 반사하는 빛을 감소시킨다.
- Fresnel equation : 프레넬 방정식은 서로 다른 표면 각에서의 표면 반사 비율을 나타낸다.
이 함수들 각각은 그들의 물리학적 요소에 대한 근사치이며 근본적인 물리학을 근사화하는 것을 목표로하는 각각의 하나 이상의 버전을
찾을 수 있다. 좀 더 현실적이고, 다른 것은 더 효율적이다. 당신이 사용하고자 하는 함수의 대략적인 버전을 선택하는 것은 완벽하게 허용된다.
Epic Games의 Brian Karis는 여러 가지 유형의 근사치에 대한 많은 연구를 수행했다. Epic Game의 Unreal Engine 4에 사용된 기능과 동일한
함수를 선택한다. 이 함수는 D용 Trowbridge-Reitz GGX, F용 Fresnel-Schlick 근사, G용 smith의 Schlick-GGX이다.
Normal distribution function
정규 분포 함수 D는 (중간) 벡터 h에 정확하게 정렬된 microfacets의 상대 표면적을 통계적으로 근사한다. 몇가지 거칠기 매개 변수가 주어지면
microfacets의 일반적인 정렬을 통계적으로 근사화하는 다수의 NDF가 정의되어 있으며 우리가 사용하게 될 것은 Trowbridge-Reitz GGX로
알려져있다:
여기서 h는 표면의 거칠기의 척도인 표면의 microfacets을 측정하기 위한 중간 벡터이다. 표면 거칠기의 매개 변수에 대해 표면 법선과
빛의 방향 사이의 중간 벡터로 h를 취하면 다음과 같은 시각적 결과를 얻는다:

거칠기가 낮으면 (표면이 매끄럽기 때문에)매우 집중된 수준의 microfacets이 작은 반경의 중간 벡터에 정렬된다. 이 높은 농도로 인해 NDF는
매우 밝은 지점을 표시한다. 그러나 거친 표면에서 microfacets이 훨씬 더 무작위 방향으로 정렬되어있는 경우, microfacets에 정렬된 훨씬
많은 수의 중간 벡터를 찾을 수 있지만 집중이 적어지면 더 많은 회색 빛 결과가 나타난다.
GLSL 코드에서 Trowbridge-Reitz GGX 정규 분포 함수는 다음과 같이 보일 것이다:
float DistributionGGX(vec3 N, vec3 H, float a)
{
float a2 = a*a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH*NdotH;
float nom = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return nom / denom;
}Geometry function
geometry 기능은 미세한 표면 세부 사항이 서로 겹쳐서 광선이 차단되는 상대 표면적을 통계적으로 근사한다.
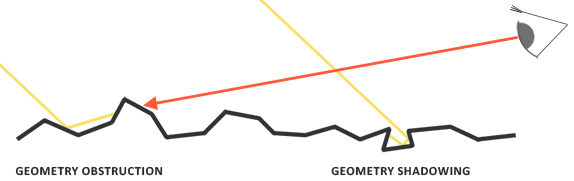
Geometry 함수는 NDF와 마찬가지로 재료의 거칠기 매개 변수를 입력으로 사용해 거친 표면을 사용해 microfacets을 음영 처리할 확률을 높인다.
우리가 사용할 기하학 함수는 Schlick-GGX로 알려진 GGX와 Schlick-Beckmann approximation의 조합이다:
여기에서 k는 direc lighting 혹은 IBL lighting에 대해 기하학 함수를 사용하는지 여부에 따라 α를 다시 맵핑한다.
α의 값은 엔진이 거칠기를 α로 변환하는 방법에 따라 다를 수 있다. 다음 튜토리얼에서는 이 재맵핑이 어떻게 관련성이 있는지,
어디서 어떻게 관련되는지에 대해 광범위하게 논의할 것이다.
geometry를 효과적으로 근사하기 위해서는 view 방향과 light 방향 벡터를 모두 고려해야한다. Smith의 방법을 사용해 두 가지를 모두 고려할
수 있다:
Schlick-GGX와 함께 Smith의 방법을 Gsub로 사용하면 거칠기 R의 변화에 따라 다음과 같은 시각적 효과를 얻을 수 있다:

기하학 함수는 [0.0, 1.0]과 흰색 또는 1.0 사이의 곱셈기이며, 미세면 그림자가 없고, 검정색 또는 0.0 완전 마이크로 표면 그림자가 있다.
GLSL에서 geometry 함수는 다음 코드로 변환된다:
float GeometrySchlickGGX(float NdotV, float k)
{
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx1 = GeometrySchlickGGX(NdotV, k);
float ggx2 = GeometrySchlickGGX(NdotL, k);
return ggx1 * ggx2;
}Fresnel equation
fresnel equation은 굴절되는 빛에 반사되는 빛의 비율을 나타내며, 이는 표면을 바라보는 각도에 따라 다르다. 빛이 표면에 부딪히는 순간
각도를 보는 표면을 기반으로해 프레넬 방정식은 반사되는 빛의 비율을 알려준다. 반사율과 에너지 보존 원리의 비율로부터 우리는 잔여
에너지로부터 빛의 굴절된 부분을 직접 얻을 수 있다.
모든 표면 또는 재료는 그 표면을 똑바로 볼 때 기본 반사도 수준을 갖지만 각도에서 표면을 볼 때 모든 반사가 표면의 기본 반사율에 비해
더 분명해진다. 수직보기 각도에서 기본 반사도가 일정한 목재/금속 책상을 보면서 자신의 모습을 직접 확인할 수 있다.
거의 90도 각도에서 책상을 보고 있으면 반사가 훨씬 더 분명해진다는 것을 알 수 있다.
완벽하게 90도 각도에서 볼 때 모든 표면은 이론적으로 빛을 완전히 반사한다. 이 현상은 Fresnel이라고 알려져 있으며
Fresnel equation에 의해 설명된다.
Fresnel equation은 다소 복잡한 방정식이지만 운 좋게도 fresnel 방정식은 fresnel-schlick 근사법을 사용해 근사할 수 있다:
Fo는 표면의 기본 반사율을 나타내며, 이는 굴절률 또는 IOR이라고 불리는 것을 사용해 계산되며 구 표면에서 볼 수 있는 것처럼 표면의
방목 각도를 볼수록(중간 시야각이 90도에 도달) fresnel과 반사가 강해진다:

프레넬 방정식에는 몇 가지 미묘한 차이가 있다. 하나는 Fresnel-Schlick 근사가 유전체 또는 비금속 표면에 대해서만 정의된다는 것이다.
도체 표면의 굴절률을 사용해 기본 반사율을 계산하는 것은 적절하게 유지되지 않으며 전도체에 대해 다른 프레넬 방정식을 사용해야한다.
이것이 불편하므로 우리는 법선 입사각(Fo)에서 표면의 응답을 미리 계산하고, Fresnel-Schlick 근사치에 따라 시야각을 기준으로 이 값을
보간함으로써 금속과 비금속에 동일한 방정식을 사용할 수 있다.
수직 입사각 또는 기본 반사율에서 표면의 반응은 Naty Hoffman의 코스 노트에서 취한 다음과 같은 일반적인 값 중 일부와 함께
대형 데이터베이스에서 찾을 수 있다:
여기에서 흥미로운 점은 모든 유전체 표면에 대해 기본 반사율이 규칙보다 예외인 0.17보다 높지 않다는 것이다.
도체의 경우 기본 반사율이 훨씬 높아지고 0.5와 1.0 사이에서 다양하다. 또한 도체 또는 금속 표면의 경우 기본 반사도가 착색되어 Fo이
RGB 삼중항으로 표시된다. 이것은 금속 표면에서만 볼 수 있다.
유전체 표면과 비교된 금속 표면의 이러한 특정 속성은 표면이 금속 표면인지 비금속 표면인지를 설명하는 금속성(metalness)이라고 하는
추가 매개 변수로 표면 물질을 작성하는 금속 워크 플로우라고 불리는 것을 발생시켰다.
유전체와 도체 모두에 대해 Fo를 사전 계산함으로써 두 가지 유형의 표면에 대해 동일한 Fresnel-Schlick 근사를 사용할 수 있지만
금속 표면이 있는 경우 기본 반사율에 색을 칠해야한다. 우리는 일반적으로 다음과 같이 이것을 수행한다:
vec3 F0 = vec3(0.04);
F0 = mix(F0, surfaceColor.rgb, metalness);우리는 대부분의 유전체 표면에 대해 근사된 기본 반사율을 정의한다. 이것은 Fo가 가장 일반적인 유전체를 중심으로 평균화된
또 다른 근사치이다. 대부분의 유전체에 대해 0.04의 기본 반사율이 유지되며 추가 표면 매개 변수를 작성하지 않고도 물리적으로 그럴듯한
결과를 생성한다. 그런 다음 금속 표면이 어떻게 되는가에 따라 유전체 기준 반사율을 취하거나 Fo를 표면색으로 표시한다.
금속 표면은 모든 굴절된 빛을 흡수하기 때문에 확산 반사가 없으므로 기본 반사율로 표면색 텍스처를 직접 사용할 수 있다.
코드에서 Fresnel Schlick 근사는 다음과 같이 변환된다:
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}cosTheta는 표면의 법선 n과 뷰 방향 v 사이의 내적 결과이다.
Cook-Torrance reflectance equation
설명된 Cook-Torrance BRDF의 모든 구성 요소를 사용해 물리적 기반 BRDF를 최종 반사 방정식에 포함할 수 있다:
그러나 이 방정식은 완전히 수학적으로 정확하지는 않다. Fresnel 항 F는 표면에서 반사되는 빛의 비율을 나타낸다. 이것은 사실 우리의
비율 ks이다. 즉, 반사율 방정식의 반사 부분이 암시적으로 반사 비율 ks를 포함한다는 것을 의미한다. 이 점을 감안할 때 최종 반사율 방정식은
다음과 같다:
이 방정식은 물리적 기반 렌더링 또는 PBR로 일반적으로 이해하는 것으로 인식되는 물리적 기반 렌더링 모델을 완벽하게 설명한다.
우리가 논의된 모든 수학을 코드에 맞추는 방법을 아직 완벽하게 이해하지 못했다고 걱정하지 말아라. 다음 튜토리얼에서 우리는 렌더링된
조명에서 훨씬 더 물리적으로 그럴듯한 결과를 얻기 위해 반사율 방정식을 이용하는 방법을 모색하고 모든 비트와 피스가 천천히 맞춰지도록해야한다.
Authoring PBR materials
PBR의 기본 수학 모델에 대한 지식을 가지고 우리는 예술가가 PBR 방정식에 직접적으로 공급할 수 있는 표면의 물리적 속성을 일반적으로
어떻게 작성하는지를 설명함으로써 토론을 마무리한다. PBR 파이프 라인에 필요한 각 표면 매개 변수는 텍스처로 정의하거나 모델링할 수 있다.
텍스처를 사용하면 각 특정 표면 점이 금속에 반응하는지, 거칠거나 부드럽든 또는 표면에 서로 다른 파장의 빛에 어떻게 반응하는지에 따라
조각마다 제어할 수 있다.
아래에서 PBR 렌더러에 공급되면 시각적 출력과 함께 PBR 파이프 라인에서 자주 볼 수 있는 텍스처 목록을 볼 수 있다:

Albedo : 알베도 텍스처는 각 텍셀에 대해 표면의 색상을 지정하거나 해당 텍셀이 금속인 경우 기본 반사도를 지정한다. 이는 확산 텍스처로
이전에 사용한 것과 거의 비슷하지만 모든 조명 정보는 텍스처에서 추출된다. 확산 텍스처는 종종 알베도 텍스처에서 원하지 않는 약간의
그림자 또는 어두워진 틈을 이미지 내에 포함한다. 표면의 색상만 포함해야한다.
Normal : 노멀 맵 텍스처는 이전의 맵핑 튜토리얼에서 사용했던 것과 똑같다. 법선 맵을 사용하면 조각을 고유한 법선으로 지정해 표면이
평평한 표면보다 울퉁불퉁하다는 환상을 부여할 수 있다.
Metalic : 메탈릭 맵은 텍셀이 메탈릭인지 아닌지를 텍셀별로 지정한다. PBR 엔진이 설정된 방식에 따라 아티스트는 그레이 스케일 값 또는
바이너리 흑백으로 금속성을 작성할 수 있다.
Roughness : 거칠기 맵은 텍셀 기준으로 표면이 얼마나 거친지를 지정한다. 거칠기의 표본 거칠기 값은 표면의 미세 표면 방향에 영향을 미친다.
더 거친 표면은 더 넓고 흐릿한 반사를 얻지만 매끄러운 표면은 집중되고 명확한 반사를 얻는다. 일부 PBR 엔진은 거친 맵 대신 매끄러운 맵을
원하지만 일부 예술가는 더 직관적이라고 판단해도 이러한 값은 샘플링되는 순간 거칠기로 변환된다.
AO : ambient occlusion 또는 AO 맵은 표면과 잠재적으로 주변 geometry의 추가 쉐도잉 팩터를 지정한다. 예를 들어, 우리가 벽돌 표면을 가지고
있다면 알베도 텍스처는 벽돌의 틈새 안에 그림자 정보가 없어야한다. 그러나 AO 지도는 빛이 빠져나가기가 더 어려워 이러한 어두운 가장자리를
지정한다. 조명 단계가 끝날 때 ambient occlusion을 고려하면 장면의 시각적 품질을 크게 향상시킬 수 있다. mesh/surface의 주변 폐색 맵은
3D 모델링 프로그램에서 수동으로 생성되거나 사전 계산된다.
아티스트는 이러한 physically based input 값을 텍셀 단위로 설정하고 조정할 수 있으며 텍스처 값을 실제 재질의 물리적 표면 특성에 기반 할 수
있다. 이는 환경이나 조명 설정에 관계없이 물리적 특성이 그럴듯한 결과를 얻도록 인위적으로 쉽게 만드는 PBR 렌더링 파이프 라인의 가장 큰 장점
중 하나이다. PBR 파이프 라인에서 작성된 표면은 서로 다른 PBR 렌더 엔진간에 쉽게 공유할 수 있으며 자신이 속한 환경에 관계없이 정확하게
보이므로 더 자연스럽게 보인다.
'Game > Graphics' 카테고리의 다른 글
| Learn OpenGL - PBR : IBL(Diffuse irradiance) (0) | 2018.10.20 |
|---|---|
| Learn OpenGL - PBR : Lighting (0) | 2018.10.20 |
| Learn OpenGL - Advanced Lighting : SSAO (0) | 2018.10.11 |
| Learn OpenGL - Advanced Lighting : Deferred Shading (0) | 2018.10.07 |
| Learn OpenGL - Advanced Lighting : Bloom (0) | 2018.10.04 |













