link : https://learnopengl.com/Advanced-Lighting/Parallax-Mapping
Parallax Mapping
Parallax Mapping은 일반적인 맵핑과 비슷한 기술이지만 다른 원칙에 기반한다. 일반 맵핑과 마찬가지로 텍스처 표면의 디테일을
대폭 향상시키고 깊이감을 주는 기법이다. 또한, 환상이지만 시차 맵핑은 깊이 감각을 전달하는데 훨씬 뛰어나며 일반 맵핑과 함께
매우 현실적인 결과를 제공한다. 시차 맵핑은 반드시 조명과 직접적으로 관련이 있는 기술은 아니지만, 이 기술은 일반적인 맵핑의
논리적인 후속 작업이므로 여기서도 논의 할 것이다. 시차 맵핑을 배우기 전에 일반 맵핑, 특히 탄젠트 공간에 대한 이해를 강력히 권장한다.
시차 맵핑은 텍스처 내부에 저장된 기하학적 정보를 기반으로 정점을 대체하거나 오프셋하느 변위 맵핑 기술 패밀리에 속한다.
이를 수행하는 한 가지 방법은 약 1000개의 정점을 가진 평면을 가져와서 특정 영역에서 평면의 높이를 알려주는 텍스처의 값에 따라
각 정점을 대체하는 것이다. 텍셀당 높이 값을 포함하는 텍스처를 높이 맵이라고 한다.
간단한 벽돌 표면의 기하학적 특성에서 파생된 높이 맵의 예는 다음과 같다:

평면 위에 걸쳐지면 각 꼭지점은 높이 맵의 샘플링된 높이 값을 기준으로 대체되어 재질의 기하학적 특성을 기반으로 평면이 거친 울퉁불퉁한
표면으로 변형된다. 예를 들어 위의 높이맵으로 대체된 평면을 가져오면 다음 이미지가 생성된다:
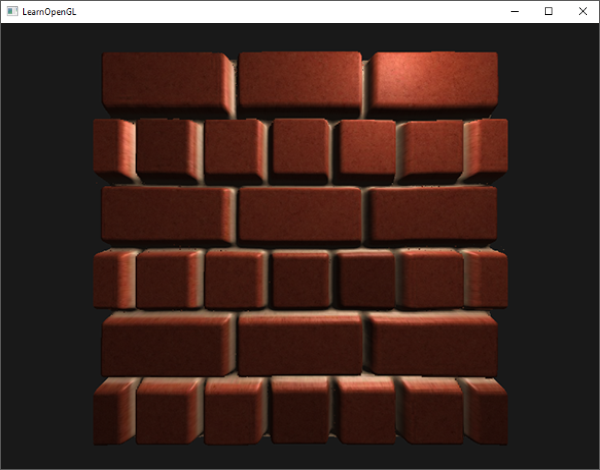
꼭지점을 옮기는 문제는 현실적인 변위를 얻기 위해 palne이 많은 양의 삼각형으로 구성되어야한다는 것이다. 그렇지 않으면
변위가 너무 거칠어 보인다. 각각의 평평한 표면이 1000개 이상의 정점을 요구할 수 있기 때문에 이것은 빠르게 계산이 불가능하다.
여분의 꼭지점이 필요없이 비슷한 사실주의를 어떻게든 얻을 수 있다면 어떨까? 사실, 위의 변위된 표면이 실제로 6개의 꼭지점으로
렌더링되었다고 당신에게 이야기한다면 어떨까? 이 벽돌 표면은 시차 맵ㅍ핑으로 렌더링됐다. 변위 맵핑 기술은 깊이를 전달하기
위해 추가 정점 데이터를 필요로 하지 않지만 일반 맵핑과 유사하게 사용자를 속이기 위한 영리한 기술을 사용한다.
시차 맵핑 뒤에 있는 아이디어는 조각의 표면이 실제보다 높거나 낮게 보이는 방식으로 텍스처 방향을 변경하는 것이다.
모든 것은 뷰 방향과 높이 맵을 기반으로 한다. 작동 원리를 이해하려면 다음과 같은 벽돌 표면의 이미지를 살펴보아라:
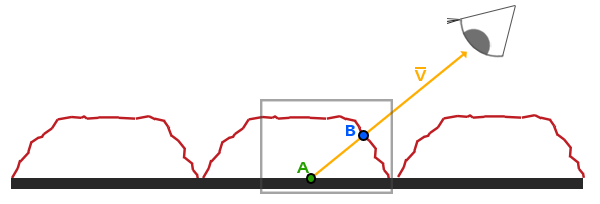
여기서 붉은 색 선은 높이 맵의 값을 벽돌 표면의 기하학적 표면 표현으로 나타내고, 벡터 V는 방향을 보는 표면을 나타낸다. (viewDir)
평면에 실제 변위가 있을 경우 관측자는 점 B에서 표면을 볼 수 있다. 그러나 평면에 실제 변위가 없으므로 뷰 방향은 평면에서
A 점으로 평평한 평면에 도달한다. 시차 맵핑은 B 지점에서 텍스처 좌표를 얻는 방식으로 조각 위치 A에서 텍스처 좌표를
오프셋하는 것을 목표로 한다. 그런 다음 모든 후속 텍스처 샘플에 대해 B점에서 텍스처 좌표를 사용해 뷰어가 실제로 보고 있는 것처럼
보이게한다.
점 A에서 점 B의 텍스처 좌표를 얻는 방법을 찾는 것이 트릭이다. 시차 맵핑은 조각 A의 높이로 fragment-to-view 방향 벡터 V를
스케일링해 이를 해결하려고 시도한다. V의 길이는 조각 위치 A에서의 높이 맵 H(A)로부터 샘플링된 값과 같아야한다.
아래 이미지는 이 스케일된 벡터 P를 보여준다:
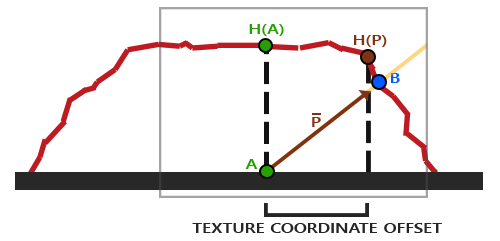
우리는 이 벡터 P를 취해 평면과 정렬된 벡터 좌표를 텍스처 좌표 오프셋으로 취한다. 이것은 벡터 P가 높이 맵의 높이 값을 사용해
계산되기 때문에 조각의 높이가 높을수록 효과적으로 대체된다.
이 작은 트릭은 대부분 좋은 결과를 주지만 근사값에 불과하다는 한계가 있다 표면의 높이가 급격하게 변하면 벡터 P가 B에 가까워지지
않을 때 결과가 비현실적으로 보인다. 당신은 아래에서 볼 수 있다:
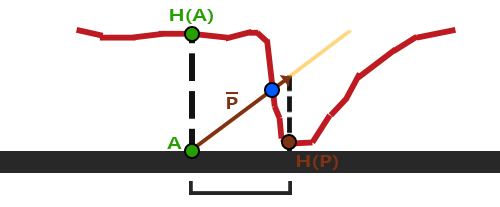
시차 맵핑의 또 다른 문제점은 표면이 어떤 방식으로든 임의로 회전 할 때 P에서 검색할 좌표를 파악하기 어렵다는 것이다.
벡터 P의 x와 y 성분이 항상 텍스처의 표면과 정렬되는 다른 좌표 공간에서의 시차 맵핑이다. 일반 맵핑 튜토리얼을 따라해본다면
아마 우리가 이 작업을 수행하는 방법을 추측했을 것이다. 우리는 접선 공간에서 시차 맵핑을 하고 싶다.
fragment-to-view 벡터 V를 접선 공간으로 변환함으로써 변환된 P 벡터는 그 표면의 탄젠트 및 접선 벡터에 정렬된 x 및 y 성분을 가질 것이다.
접선 벡터와 접하는 벡터가 표면의 텍스처 좌표와 같은 방향을 가리키고 있기 때문에 표면의 방향에 관계없이 P의 x 및 y 구성 요소를 텍스처
좌표 오프셋으로 사용할 수 있다.
그러나 이론에 대해서 충분히 생각해보자. 우리의 발을 젖게하고 실제 시차 맵핑을 구현하기 시작하자.
Parallax mapping
시차 맵핑의 경우 우리는 접선과 접선 벡터를 계산한 간단한 2D 평면을 GPU로 보내기 전에 이것을 사용할 것이다. 우리가 일반적인 맵핑
튜토리얼에서 했던 것과 비슷하다. 이 예제에서는 일반 맵핑과 함께 시차 맵핑을 사용한다. 시차 맵핑은 표면을 대체한다는 환상을 주기
때문에 조명이 일치하지 않으면 환상이 깨진다. 노멀 맵은 종종 높이 맵에서 생성되기 때문에 높이 맵과 함께 노멀 맵을 사용하면 조명이
displacement와 함께 자기 위치에 있는지 확인할 수 있다.
위에 연결된 변위 맵이 이 튜토리얼의 시작 부분에 표시된 높이 맵의 역이라고 이미 언급했을 것이다. 시차 맵핑을 사용하면 평평한 표면의
높이보다 가짜 깊이를 쉽게 만드는 것처럼 높이 맵의 역수를 사용하는 것이 더 적합하다. 이것은 아래와 같이 시차 맵핑을 인식하는
방식을 약간 변경한다:
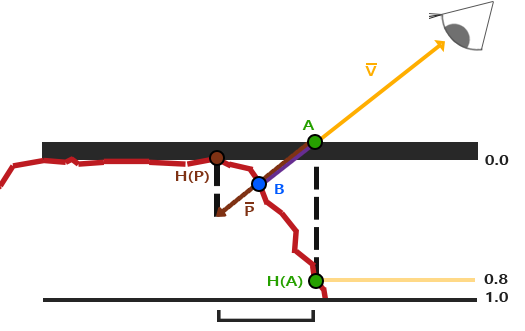
우리는 다시 점 A와 B를 가지지만 이번에는 점A의 텍스처 좌표에서 벡터 V를 뺀 벡터 P를 얻는다. 우리는 쉐이더에서 1.0 샘플된
높이 맵 값을 뺀 높이 값 대신에 깊이 값을 얻을 수 있다. 또는 위에 링크된 깊이 맵에서 했던 것처럼 이미지 편집 소프트웨어에서
단순히 텍스처 값을 반대로 변경하는 것이다.
변위 효과는 삼각형 표면 전체에서 다르기 때문에 시차 맵핑은 조각 쉐이더에서 구현된다. 조각 쉐이더에서는 fragment-to-view 벡터 V를
계산해야하므로 접선 공간에서 뷰 위치와 조각 위치가 필요하다. 일반 맵핑 튜토리얼에서 접선 공간에 이러한 벡터를 보내는 조각 쉐이더가
이미 있으므로 이 튜토리얼의 정점 쉐이더의 정확한 복사본을 얻을 수 있다:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
uniform vec3 lightPos;
uniform vec3 viewPos;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
vs_out.TexCoords = aTexCoords;
vec3 T = normalize(mat3(model) * aTangent);
vec3 B = normalize(mat3(model) * aBitangent);
vec3 N = normalize(mat3(model) * aNormal);
mat3 TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vs_out.FragPos;
} 주목할 점은 시차 맵핑의 경우 aPos와 뷰어의 위치 viewPos를 접선 공간에 조각 쉐이더로 보내야한다는 것이다.
조각 쉐이더 내에서 우리는 시차 맵핑 로직을 구현한다. 조각 쉐이더는 다음과 같이 보인다:
#version 330 core
out vec4 FragColor;
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} fs_in;
uniform sampler2D diffuseMap;
uniform sampler2D normalMap;
uniform sampler2D depthMap;
uniform float height_scale;
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir);
void main()
{
// offset texture coordinates with Parallax Mapping
vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos);
vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir);
// then sample textures with new texture coords
vec3 diffuse = texture(diffuseMap, texCoords);
vec3 normal = texture(normalMap, texCoords);
normal = normalize(normal * 2.0 - 1.0);
// proceed with lighting code
[...]
}우리는 ParallaxMapping이라는 함수를 정의했다. 이 함수는 접선 공간에서 조각의 텍스처 좌표와 fragment-to-view V를 입력으로 취한다.
이 함수는 이동된 텍스처 좌표를 반환한다. 그런 다음 이러한 이동된 텍스처 좌표를 혹산 및 법선 맵을 샘플링하기 위한 좌표로 사용한다.
결과적으로 조각의 확산 색상 및 법선 벡터는 표면의 배치된 형상과 동일하게 일치한다.
ParallaxMapping 함수를 살펴보자:
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{
float height = texture(depthMap, texCoords).r;
vec2 p = viewDir.xy / viewDir.z * (height * height_scale);
return texCoords - p;
} 이 비교적 간단한 함수는 지금까지 논의한 것을 직접 번역한 것입니다. 원래 텍스처 좌표인 texCoords를 가져와서 이것을 사용해
현재 조각 H (A)의 depthMap에서 높이를 샘플링한다. 그런 다음 pang을 접선 공간의 viewDir벡터의 x,y 구성 요소로 z 구성 요소를 나눈 값으로
계산하고 조각 높이로 스케일한다. 시차 효과는 일반적으로 여분의 눈금 매개 변수없이 너무 강하기 때문에 일부 추가 컨트롤을 위해
height_scale 유니폼을 도입했다. 그런 다음 텍스쳐 좌표에서 이 벡터 P를 빼서 최종 치환된 텍스처 좌표를 얻는다.
흥미로운 점은 viewDir.xy에 의해 viewDir.xy의 분할이 있다는 것이다. viewDir 벡터가 정규화되면 viewDir.z는 0.0과 1.0 사이의 어딘가에 위치한다.
viewDir이 표면과 대체로 평행 할 때 z 컴포넌트는 0.0에 가깝고 division은 viewDir이 표면에 대체로 수직일 때보다 훨씬 더 큰 벡터 P를 반환한다.
그래서 기본적으로 우리는 꼭대기에서 보았을 때와 비교할 때 각도에서 표면을 볼 때 더 큰 스케일에서 텍스처 좌표를 오프셋하는 방식으로
P의 크기를 늘린다. 각도에서 보다 사실적인 결과를 제공한다. 어떤 사람들은 일반적인 시차 맵핑이 각도에서 바람직하지 않은 결과를
생성할 수 있으므로 방정식에서 viewDir.z로 나누기를 선호한다. 이 기술은 오프셋 한계가 있는 시차 맵핑이라고 한다. 선택해야 할 기법을
선택하는 것은 대개 개인적인 취향에 달려 있지만 보통 Parallax Mapping을 사용하는 경향이 있다.
결과 텍스처 좌표는 다른 텍스처를 샘플링하는 데 사용되며 아래에서 height_scale이 대략 0.1인 것으로 볼 수 있는 것처럼 아주 깔끔한
대체 효과를 제공한다:
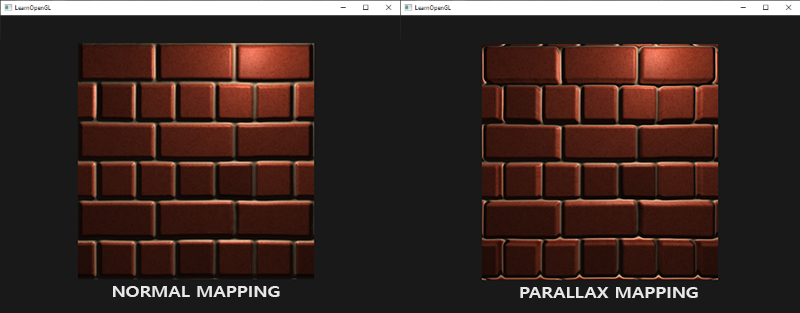
여기서 노멀 맵핑과 시차 맵핑의 차이점을 볼 수 있다. 시차 맵핑은 깊이를 시뮬레이트 하기 때문에 실제로 보는 방향에 따라 다른 벽돌과
벽돌을 겹치게 하는 것이 가능하다.
시차 맵핑된 평면의 가장자리에서 여전히 이상한 테두리 인공물을 볼 수 있다. 이것은 평면의 가장자리에서 변위가 적용된 텍스처 좌표가
[0,1] 범위를 초과해 오버 샘플링 할 수 있기 때문에 텍스처의 배치 모드를 기반으로 비현실적인 결과를 나타내서 발생한다. 이 문제를 해결하기
위한 멋진 트릭은 기본 텍스처 좌표 범위를 벗어나 샘플링 할 때마다 조각을 버리는 것이다:
texCoords = ParallaxMapping(fs_in.TexCoords, viewDir);
if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0)
discard;기본 범위 밖의 텍스처 좌표를 가진 모든 조각은 버려지고, Parallax Mapping은 표면의 가장자리 주위에서 적절한 결과를 제공한다.
이 트릭은 모든 유형의 표면에서 제대로 작동하지 않지만 plane에 적용하면 평면이 실제로 사라지는 것처럼 보이게 하는 훌륭한
결과를 제공한다:
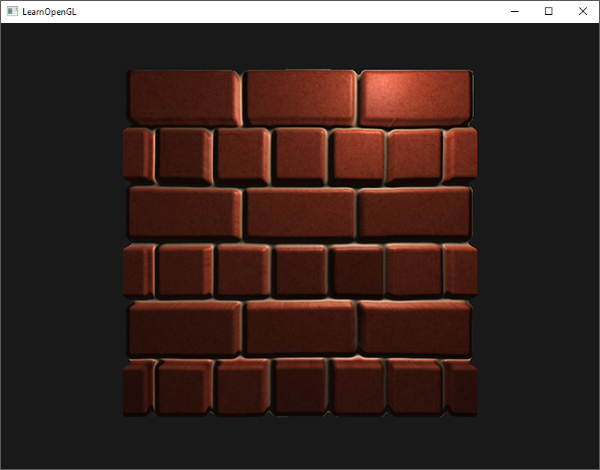
멋지게 보이고 아주 빠르다. 시차 맵핑을 작동시키기 위해 여분의 텍스처 샘플 하나만 있으면 된다. 몇 가지 문제가 있다.
특정 각도에서 보았을 때 일그러지고 아래에서 보듯이 가파른 높이 변화가 있는 잘못된 결과가 나타난다.
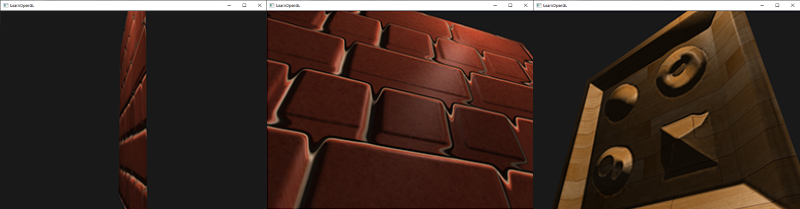
그것이 때때로 제대로 작동하지 않는 이유는 그것이 변위 맵핑의 근본적인 근사일 뿐이기 때문이다. 그러나 가파른 높이 변화에도 거의 완벽한
결과를 얻을 수 있는 몇 가지 추가 트릭이 있다. 예를 들어, 하나의 표본 대신에 B에 가장 가까운 점을 찾기 위해 여러 표본을 취하면 어떨까?
Steep Parallax Mapping
Steep Parallax Mapping은 동일한 원칙을 사용한다는 점에서 Parallax Mapping의 확장이다. 그러나 1 샘플 대신 벡터 P를 B에 더
정확하게 나타내기 위해 여러 샘플을 필요로 한다. 이것은 가파른 높이 변화로도 훨씬 좋은 결과를 제공한다. 기술의 정확성은
샘플 수만큼 향상된다.
Steep Parallax Mapping의 일반적인 개념은 전체 깊이 범위를 동일한 높이/깊이의 여러 레이어로 나누는 것이다. 이 레이어들 각각에 대해
우리는 현재 레이어의 깊이 값보다 낮은 샘플링된 깊이 값을 찾을 때까지 텍스처 좌표를 P 방향으로 시프트하는 깊이 맵을 샘플링한다.
다음 이미지를 살펴보자:
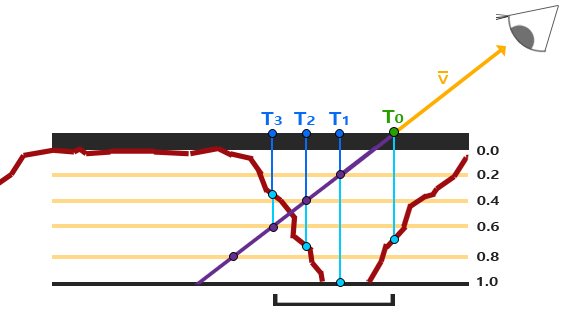
깊이 레이어를 위에서 아래로 가로 지르며 각 레이어에 대해 깊이 값을 깊이 맵에 저장된 깊이 값과 비교한다.
레이어의 깊이 값이 깊이 맵의 값보다 작으면 이 레이어의 벡터 P의 일부가 표면 아래에 있지 않다는 것을 의미한다.
레이어의 깊이가 깊이 맵에 저장된 값보다 높을 때까지 이 과정을 계속한다. 이 점은 기하하적인 표면 아래에 있다.
이 예제에서 우리는 두 번째 레이어의 깊이 맵 값 (D (2) = 0.73)이 두 번째 레이어의 깊이 값 0.4보다 여전히 낮아서 계속 진행할 수
있음을 알 수 있다. 다음 반복에서 레이어의 깊이 값 0.6은 깊이 맵의 샘플 깊이 값 (D(3) = 0.37)보다 높아진다.
따라서 우리는 제 3층이 벡터 P가 변위된 기하학 트리의 가장 실용적인 위치라고 가정 할 수 있다. 우리는 벡터 P3에서 텍스처 좌표
오프셋 T3를 취해 조각의 텍스처 좌표를 대체 할 수 있다. 깊이가 더 깊어지면 정확도가 어떻게 증가하는지 볼 수 있다.
이 기술을 구현하기 위해 필요한 모든 변수가 이미 있으므로 ParallaxMapping 함수만 변경된다:
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{
// number of depth layers
const float numLayers = 10;
// calculate the size of each layer
float layerDepth = 1.0 / numLayers;
// depth of current layer
float currentLayerDepth = 0.0;
// the amount to shift the texture coordinates per layer (from vector P)
vec2 P = viewDir.xy * height_scale;
vec2 deltaTexCoords = P / numLayers;
[...]
} 여기에서는 먼저 레이어 수를 지정하고 각 레이어의 깊이를 계산한 다음 레이어당 P 방향을 따라 이동해야 하는 텍스처 좌표 오프셋을
계산한다.
레이어의 깊이 값보다 작은 depthmap 값을 찾을 때까지 위에서부터 모든 레이어를 반복한다:
// get initial values
vec2 currentTexCoords = texCoords;
float currentDepthMapValue = texture(depthMap, currentTexCoords).r;
while(currentLayerDepth < currentDepthMapValue)
{
// shift texture coordinates along direction of P
currentTexCoords -= deltaTexCoords;
// get depthmap value at current texture coordinates
currentDepthMapValue = texture(depthMap, currentTexCoords).r;
// get depth of next layer
currentLayerDepth += layerDepth;
}
return currentTexCoords;여기에서 우리는 각 깊이 레이어를 반복하고, 벡터 P를 따라 텍스처 좌표 오프셋을 찾을 때까지 정지한다. 처음에는 표면 아래의 깊이를
반복한다. 최종 오프셋된 텍스처 좌표 벡터를 얻기 위해 조각의 텍스처 좌표에서 결과 오프셋을 뺀다. 이 시간은 전통적인 시차 맵핑과 비교해
훨씬 더 정확하다.
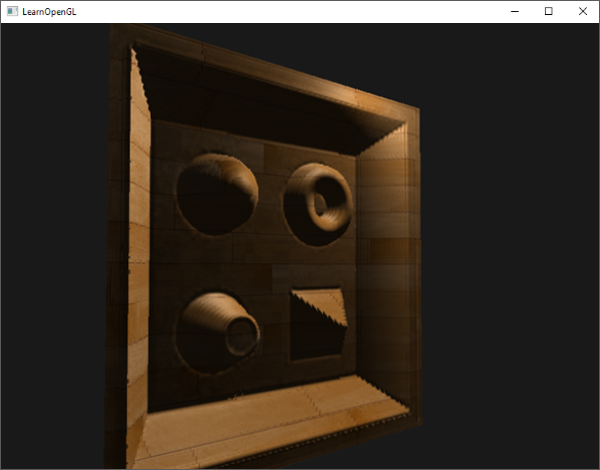
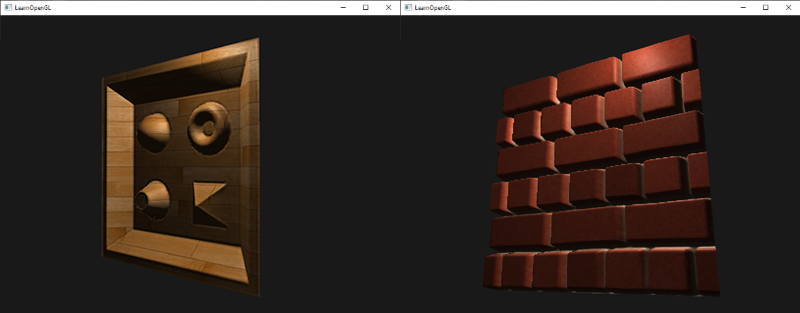
약 10개의 샘플을 사용하면 벽돌 표면이 이미 각도에서 보았을 때보다 더 실용적으로 보인다. 그러나 갑작스런 시차 맵핑은 이전에 표시된
나무 장난감 표면과 같이 가파른 높이 변화가 있는 복잡한 표면을 가질 때 정말 빛난다:
Parallax Mapping의 속성 중 하나를 이용해 알고리즘을 조금 개선할 수 있따. 표면에 직선으로 보았을 때 텍스처 변위는 별로 일어나지
않지만 각도를 틀어서 표면을 볼 때 많은 변위가 발생한다. 각을 직선으로 볼 때 샘플을 적게 사용하고 각을 틀어서 볼 때 샘플을 더 많이
취함으로써 필요한 양만 샘플링한다:
const float minLayers = 8.0;
const float maxLayers = 32.0;
float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir))); 여기에서 viewDir과 양의 z 방향의 내적을 취해 그 결과를 사용해 표면을 바라보는 각도를 기준으로 샘플 수를 minLayers 또는
maxLayers에 정렬한다. 우리가 표면에 평행한 방향을 보려고 한다면 총 32개의 레이어를 사용할 것이다.
Steep Parallax Mapping 역시 문제가 있다. 이 기술은 한정된 수의 샘플을 기반으로 하기 때문에 앨리어싱 효과를 얻고
레이어 간의 명확한 구분을 쉽게 발견 할 수 있다:
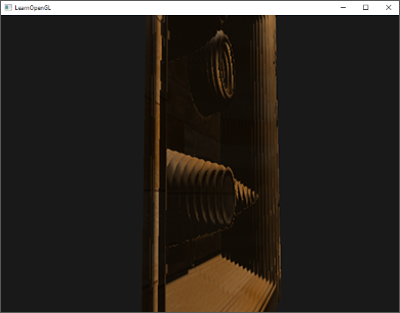
더 많은 수의 샘플을 사용해 문제를 줄일 수 있지만 성능에 너무 큰 부담이 된다. 표면 아래에 있는 첫 번째 위치를 취하지 않고
B에 훨씬 더 가까운 일치를 찾기 위해 위치의 가장 가가운 두 깊이 레이어를 보간해 이 문제를 해결하는 것을 목표로 하는 여러 접근법이 있다.
이러한 접근 방식 중 가장 인기있는 두 가지를 Relief Parallax Mapping 및 Parallax Occlusion Mapping 이라고 하며 Relief Parallax Mapping은
가장 정확한 결과를 제공하지만 Parallax Occlusion Mapping과 비교할 때 성능이 훨씬 뛰어나다. Parallax Occlusion Mapping은
Relief Parallax Mapping과 거의 동일한 결과를 제공하기 때문에 더 효율적이다. 종종 선호되는 접근 방법이며 마지막으로 Parallax Mapping 유형이다.
Parallax Occlusion Mapping
Parallax Occlusion Mapping은 Steep Parallax Mapping과 같은 원칙을 기반으로 하지만, 충돌 후 첫 번째 깊이 레이어의 텍스처 좌표를
가져오는 대신 충돌 후와 깊이 레이어 사이를 선형으로 보간하려고 한다. 선형 보간의 가중치는 표면의 높이가 깊이 레이어의 두 레이어 값과
얼마나 떨어져 있는지를 기준으로 한다. 어떻게 작동하는지 파악하기 위해 다음 사진을 보아라:
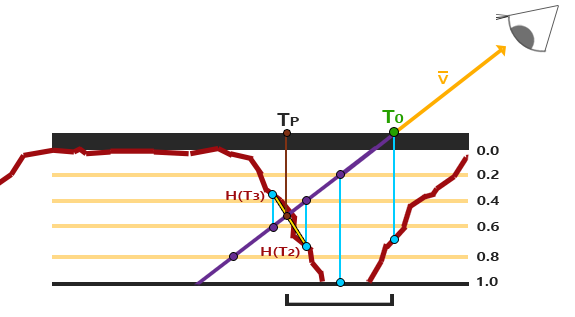
보시다시피 Steep Parallax Mapping과 거의 비슷하다. 이 단계는 교차점을 둘러싼 두 개의 깊이 레이어의 텍스처 좌표간의
선형 보간을 추가로 수행한다. 이것은 근사값이지만 Steep Parallax Mapping 보다 훨씬 더 정확하다.
Parallax Occlusion Mapping의 코드는 Steep Parallax Mapping의 맨 위에 있는 확장이며 그리 어렵지 않다:
[...] // steep parallax mapping code here
// get texture coordinates before collision (reverse operations)
vec2 prevTexCoords = currentTexCoords + deltaTexCoords;
// get depth after and before collision for linear interpolation
float afterDepth = currentDepthMapValue - currentLayerDepth;
float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth;
// interpolation of texture coordinates
float weight = afterDepth / (afterDepth - beforeDepth);
vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight);
return finalTexCoords; 표면 기하를 교차시킨 후 깊이 레이어를 찾은 후에는 교차하기 전에 깊이 레이어의 텍스처 좌표를 검색한다.
다음으로 우리는 대응하는 깊이 레이어들로부터 기하의 깊이 거리를 계산하고 이 두 값들 사이를 보간한다. 선형 보간은 두 레이어의 텍스처
좌표 간의 기본 보간이다. 함수는 마지막으로 최종 보간된 텍스처 좌표를 반환한다.
Parallax Occlusion Mapping은 놀라울 정도로 좋은 결과를 제공한다. 약간의 인공물과 앨리어싱 문제는 여전히 눈에 띄지만 전반적으로
좋은 트레이드 오프이며 매우 심하게 확대하거나 매우 가파른 각도를 볼 때만 볼 수 있다.
시차 맵핑은 장면의 세부 묘사를 향상시키는 훌륭한 기술이지만 이를 사용할 때 고려해야할 몇 가지 인공물이 있다.
대부분의 경우 시차 맵핑은 바닥이나 벽과 같은 표면에 사용된다. 표면의 윤곽선을 쉽게 결정할 수 없으며 시야각은 일반적으로 표면에 대략
직각이다. 이 방법으로 Parallax Mapping의 유물은 눈에 띄지 않게 되어 객체의 세부 묘사를 향상시키는 매우 흥미로운 기술이 된다.
'Game > Graphics' 카테고리의 다른 글
| Learn OpenGL - Advanced Lighting : Bloom (0) | 2018.10.04 |
|---|---|
| LearnOpenGL - Advanced Lighting : HDR (0) | 2018.10.03 |
| Learn OpenGL - Advanced Lighting : Normal Mapping (2) | 2018.10.01 |
| Learn OpenGL - Advanced Lighting : Point Shadows (2) (0) | 2018.10.01 |
| Learn OpenGL - Advanced Lighting : Point Shadows (1) (0) | 2018.09.27 |

