link : https://learnopengl.com/Advanced-Lighting/Normal-Mapping
Normal Mapping
우리의 모든 장면은 수백 또는 수천 개의 평면 삼각형으로 구성된 다각형으로 채워져 있다. 우리는 이 평평한 삼각형에 2D 텍스처를
붙여서 사실성을 높이고, 폴리곤이 실제로 작은 평평한 삼각형으로 이루어져 있다는 사실을 숨기고 추가 세부 사항을 제공한다.
하지만 텍스처를 자세히 보면 아주 평평한 표면을 볼 수 있다. 실제 표면의 대부분은 평면이 아니며 많은 울퉁불퉁한 세부 사항을 나타낸다.
예를 들어, 벽돌 표면을 보자. 벽돌 표면은 상당히 거친 표면이며 분명히 완전히 평평하지 않다. 그것은 침몰한 시멘트 줄무늬와 상세한
작은 구멍과 균열을 많이 포함한다. 우리가 조명이 있는 장면에서 그런 벽돌 표면을 보았다면 몰입감은 쉽게 깨진다.
아래에서 점 광원에 의해 점등되는 평평한면에 적용된 벽돌 텍스처를 볼 수 있다.
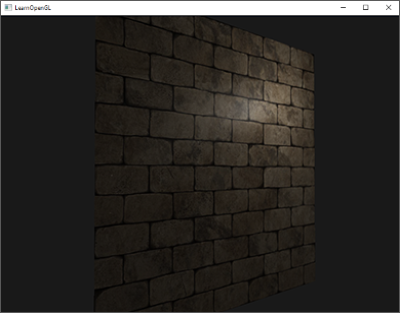
조명은 작은 균열과 구멍을 고려하지 않고 벽돌 사이의 깊은 줄무늬를 완전히 무시한다. 표면은 완전히 평평하게 보인다.
specular 맵을 사용해 깊이나 기타 세부 사항으로 인해 조명이 덜한 표면을 가장함으로써 평면도를 부분저긍로 해결할 수 있지만
이는 실제 솔루션보다 해킹이다. 조명 시스템에 표면의 작은 깊이와 같은 세부 사항을 알려주는 방법이 필요하다.
우리가 빛의 관점에서 이것을 생각한다면 : 표면이 어떻게 완전히 평평한 표면으로 켜지는가? 답은 표면의 법선 벡터이다.
조명 알고리즘의 관점에서 객체의 모양을 결정하는 유일한 방법은 수직 법선 벡터에 의한 것이다.
벽돌 표면에는 하나의 법선 벡터만 있으므로 이 법선 벡터의 방향에 따라 표면이 균일하게 조명된다. 표면당 법선 대신 각 조각마다
동일한 경우 각 조각마다 다른 조각 별 법선을 사용하면 어떨까? 이 방법으로 표면의 작은 세부 사항을 기반으로 법선 벡터를 약간 벗어날
수 있다. 결과적으로 이것은 표면이 훨씬 더 복잡하다는 착각을 일으킨다:

조각마다 법선을 사용함으로써 조명을 속여 작은 표면 (수직벡터에 수직)으로 구성된 표면이 표면에 엄청난 향상을 준다고 믿게 만든다.
표면당 법선과 비교한 각 조각별 법선을 사용하는 이 기법을 일반 매핑 또는 범프 매핑이라고 한다. 벽돌 평면에 적용하면 다음과 같이 보인다:
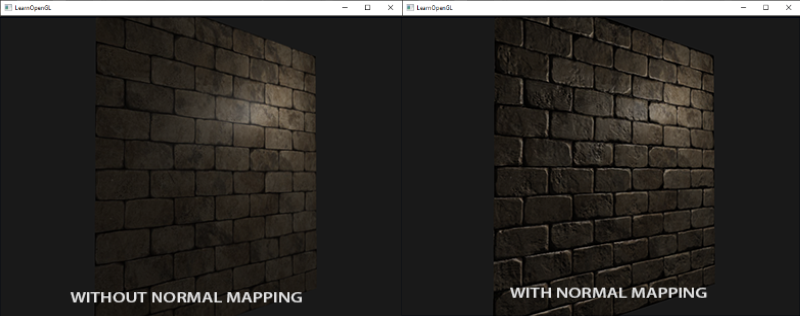
보시다시피, 세부적인 면과 비용면에서 엄청난 향상을 가져온다. 우리는 조각당 법선 벡터만 변경하기 때문에 조명 방정식을 변경할
필요가 없다. 조명 알고리즈멩 수직인 보간된 표면 대신 조각당 법선을 전달한다. 조명은 표면에 디테일을 제공한다.
Normal mapping
정상적인 맵핑을 작동시키려면 조각당 법선이 필요하다. diffuse 맵과 specular 맵을 사용한 것과 비슷하게 우리는 2D 텍스처를 사용해
조각당 데이터를 저장할 수 있다. 색상 및 조명 데이터 외에도 법선 벡터를 2D 텍스처로 저장할 수 있다. 이 방법을 사용하면 2D 텍스처에서
샘플을 추출해 특정 조각에 대한 법선 벡터를 얻을 수 있다.
법선 벡터는 기하학적 엔티티이고 텍스처는 일반적으로 텍스처의 법선 벡터를 저장하는 색상 정보에만 사용된다. 즉각적인 것은 아니다.
텍스처의 색상 벡터를 생각하면 r,g,b 구성 요소가 있는 3D 벡터로 표현된다. 우리는 마찬가지로 법선 벡터의 x,y,z 구성 요소를 각 색상 구성
요소에 저장할 수 있다. 노멀 벡터의 범위는 -1과 1 사이이므로 먼저 [0,1]에 맵핑된다:
vec3 rgb_normal = normal * 0.5 + 0.5; // transforms from [-1,1] to [0,1] 이와 같이 RGB 벡터로 변환된 법선 벡터를 사용해 표면의 모양에서 파생된 조각 단위의 법선을 2D 텍스처에 저장할 수 있다.
이 튜토리얼의 시작 부분에 있는 벽돌 표면의 예제 노멀 맵은 아래와 같다:

이에는 파란 색조가 있다. 이것은 모든 법선이 (0, 1, 1)인 양의 z축을 향해 바깥쪽으로 가깝게 향하기 때문이다.
색상의 조금 편차는 일반적인 양의 z 방향에서 약간 오프셋된 법선 벡터를 나타내며 텍스처에 깊이감을 부여한다.
예를 들어, 각 벽돌의 맨 위에 있는 색상은 더 많은 녹색을 띄는 경향이 있다. 벽돌의 윗면이 양의 y 방향 (0,1,0)으로 더 많이
가리키는 법선을 가질 때 의미가 있다.
z 축의 양의 방향을 바라보는 간단한 평면을 사용하면 이 확산된 텍스처와 노멀 맵을 사용해 이전 섹션의 이미지를 렌더링할 수 있다.
연결된 노멀 맵은 위에 표시된 맵과 다르다. 그 이유는 OpenGL은 텍스처가 일반적으로 만들어지는 방식고 ㅏ반대인 y 좌표로 텍스처 좌표를
읽기 때문이다. 연결된 노멀 맵은 y 컴포넌트를 반전시킨다. 이것을 고려하지 않으면 조명이 올바르지 않다.
두 텍스처를 모두 로드하고 적절한 텍스처 단위에 바인딩한 다음 조명 조각 쉐이더에서 다음과 같이 변경해 평면을 렌더링한다:
uniform sampler2D normalMap;
void main()
{
// obtain normal from normal map in range [0,1]
normal = texture(normalMap, fs_in.TexCoords).rgb;
// transform normal vector to range [-1,1]
normal = normalize(normal * 2.0 - 1.0);
[...]
// proceed with lighting as normal
} 여기서는 [0,1]의 샘플된 표준 색상을 다시 [-1,1]로 다시 맵핑하고 곧 나오는 조명 계산에 샘플링된 법선 벡터를 사용해 법선을
RGB 색상에 맵핑하는 과정을 뒤집는다. 이 경우 Blinn-Phong 쉐이더를 사용했다.
시간이 지남에 따라 광원을 천천히 움직이면 법선 맵을 사용해 깊이감을 느낄 수 있다. 이 일반 맵핑 예제를 실행하면 이 튜토리얼의 시작
부분에 표시된 것과 같은 정확한 결과를 얻을 수 있다:
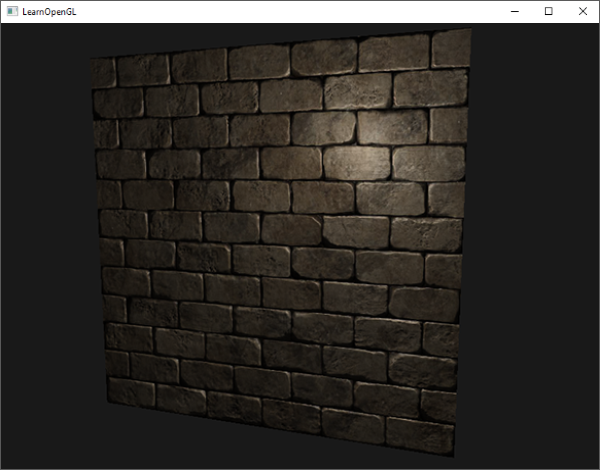
그러나 노멀 맵의 사용을 크게 제한하는 한 가지 문제가 있다. 우리가 사용한 노멀 맵은 z 방향이 양의 방향을 가리키는
법선 벡터를 가진다. 이것은 비행기의 표면 법선이 z 방향의 양의 방향을 가리키고 있기 때문에 효과가 있었다.
그러나 양의 y 방향을 가리키는 표면 법선 벡터를 사용해 바닥에 놓인 평면에서 동일한 노멀 맵을 사용하면 어떻게 될까?
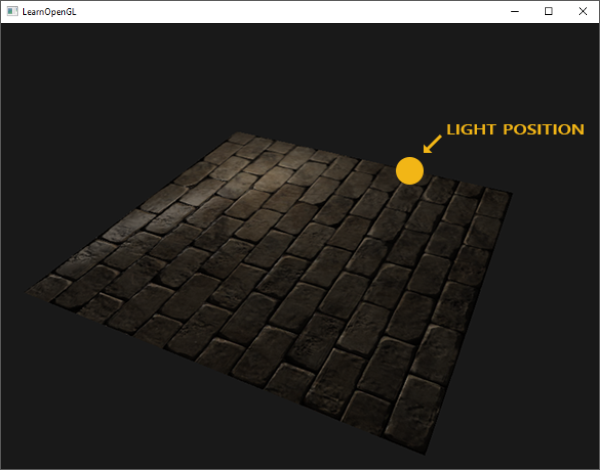
조명이 제대로 보이지 않는다! 이것은 표면 법선의 양의 y 방향을 약간 가리키지만 이 평면의 샘플된 법선이 여전히
z축의 양의 방향을 향하기 때문에 발생한다. 결과적으로 조명은 표면의 법선이 여전히 양의 z 방향을 보고 있을 때와 같다고 생각한다.
아래 이미지는 샘플된 법선이 이 표면에 대략 어떻게 보이는지 보여준다:

모든 법선은 양의 y 방향에서 표면 법선을 따라 가리켜야 하면서 양의 z방향을 대략적으로 가리키는 것을 볼 수 있다.
이 문제에 대한 가능한 해결책은 표면의 가능한 각 방향에 대한 법선 맵을 정의하는 것이다. 큐브의 경우 우리는 6개의 노멀 맵이
필요하지만 가능한 수백 개의 표면 방향을 가질 수 있는 고급 모델을 사용하면 이것이 실행 불가능한 방법이 된다.
다른 좌표 공간에서 점등을 하면 다르고 더 어려운 해결책이 가능하다: 법선 벡터가 항상 양의 z 방향을 가리키는 좌표 공간;
다른 모든 조명 벡터는 이 양의 z 방향에 대해 상대적으로 변환된다. 이렇게 하면 방향에 관계없이 항상 동일한 법선 맵을
사용할 수 있다. 이 좌표 공간을 접선 공간이라고 한다.
Tangent space
법선 벡터는 법선이 항상 양의 z 방향을 가리키는 탄젠트 공간에서 표현된다. 탄젠트 공간은 삼각형의 표면에 국한된 공간이다.
법선은 개별 삼각형의 로컬 참조 프레임을 기준으로 한다. 그것을 노멀 맵 벡터의 로컬 공간으로 생각해라. 최종 변환된 방향에
관계없이 모두 양의 z 방향을 가리키는 것으로 정의된다. 특정 행렬을 사용해 법선 벡터를 이 로컬 접선 공간에서 월드 또는 뷰 좌표로
변환해 최종 맵핑된 표면의 방향을 따라 방향을 지정한다.
양수 y 방향을 바라보는 이전 섹션의 부정확한 법선 맵핑 표면이 있다고 가정해보자. 노멀 맵은 접선 공간에서 정의된다.
따라서 문제를 해결하는 한 가지 방법은 법선을 접선 공간에서 다른 공간으로 변형해 표면의 법선 방향과 정렬되도록 하는
행렬을 계산하는 것이다. 법선 벡터가 모두 가리키는 경우 대체로 양의 y 방향이다. 접하는 공간에 대한 가장 좋은 점은
접선 공간의 z 방향을 표면의 법선 방향에 올바르게 맞출 수 있도록 모든 유형의 표면에 대해 이러한 행렬을 계산할 수 있다는 것이다.
이러한 행렬은 TBN 행렬이라 불리며 문자는 Tangent-Bitangent-Normal vector를 나타낸다. 이것들은 이 행렬을 구성하는데 필요한 벡터이다.
탄젠트 공간 벡터를 다른 좌표 공간으로 변환하는 기저 변환 행렬을 구성하려면 법선 맵의 표면을 따라 정렬된 3개의 수직 벡터가 필요하다.
위쪽, 오른쪽, 전방 벡터; 우리가 카메라 튜토리얼에서 했던 것과 비슷하다.
우리는 이미 표면의 법선 벡터인 up 벡터를 알고 있다. 오른쪽 벡터와 전방 벡터는 각각 접선과 반대 벡터이다.
표면의 다음 이미지는 표면의 세 벡터를 모두 보여준다:
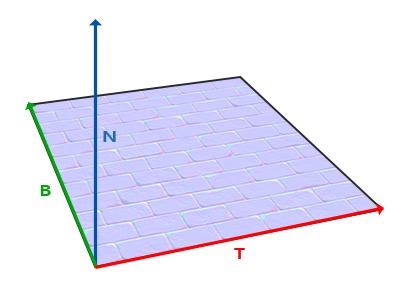
탄젠트 및 비트 탄젠트 벡터를 계산하는 것은 법선 벡터만큼 간단하지 않다. 우리는 법선 맵의 접선과 접하는 벡터의 방향이
표면의 텍스처 좌표를 정의하는 방향과 정렬된다는 것을 이미지에서 볼 수 있다. 우리는 이 사실을 사용해 각 표면에 대한
접선 및 비트 탄젠트 벡터를 계산한다. 그것들을 가져오려면 약간의 수학이 필요하다. 다음 이미지를 살펴보자:
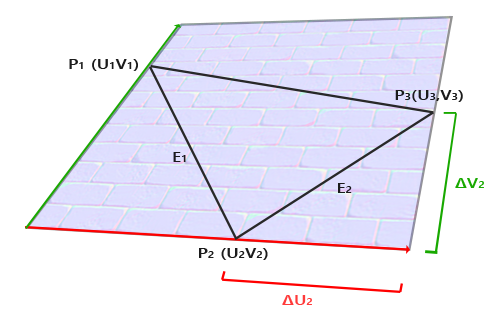
그림에서 우리는 삼각형의 가장자리 E2의 텍스처 좌표 차이가 ΔU2로 표시되고 ΔV2가 접선 벡터 T와 비트 벡터 B와 같은
방향으로 표시된다는 것을 알 수 있다. 이 때문에 표시되는 가장자리 E1과 삼각형의 E2는 접선 벡터 T와 접선 벡터 B의
선형 조합으로 나타낸다. B : 표면의 텍스처 좌표를 정의하는 방향이다.
우리는 이 사실을 사용해 각 표면에 대한 접선 및 비트 탄젠트 벡터를 계산한다. 그것들을 가져 오려면 약간의 수학이 필요하다.
다음 이미지를 살펴보아라:
이것은 다음과 같이 쓸 수도 있다:
두 벡터 위치 사이의 차이 벡터와 ΔU와 ΔV를 텍스처 좌표 차이로 계산할 수 있다. 우리는 두 개의 미지수 (접선 T와 B의 접선)와 두 개의
방정식을 남긴다. 대수학 수업에서 T와 B를 풀 수 있다는 것을 기억해야한다.
마지막으로 방정식으로 우리는 그것을 다른 형태로 쓸 수 있다:
머리에 행렬 곱셈을 시각화하고 실제로 이것이 같은 방정식인지 확인해라. 방정식을 행렬 형태로 재작성하는 이점은 T와 B에 대한
해결이 훨씬 더 분명해진다는 것이다. 방정식의 양변에 ΔUΔV 행렬의 역을 곱하면 다음과 같이 된다:
이것은 T와 B를 풀 수 있게 해준다. 델타 텍스처 좌표 행렬의 역함수를 계산해야한다. 나는 역행렬을 계산하는 수학적 세부 사항을
다루지는 않겠지만, 행렬의 행렬식에 행렬식을 곱한 행렬식에 대한 대략 1로 변환된다:
이 마지막 방정식은 삼각형의 두 가장자리와 텍스처 좌표에서 접선 벡터 T와 접선 벡터 B를 계산하는 수식을 제공한다.
이 배후에 있는 수학을 정말로 이해하지 못한다고 해서 걱정하지 말아라. 삼각형의 꼭지점과 그 텍스처 좌표에서 접선과 비트를
계산할 수 있다는 것을 이해한다면 (텍스처 좌표는 접선 벡터와 같은 공간에 있기 떄문에) 절반은 왔다.
Manual calculation of tangents and bitangents
튜토리얼의 데모 장면에서 우리는 양의 z 방향을 바라보는 간단한 2D 평면을 보았다. 이번에는 탄젠트 공간을 사용하는 일반
맵핑을 구현하고 싶지만 이 평면을 원한다면 방향을 지정할 수 있지만 정상 맵핑은 여전히 작동한다.
앞에서 언급한 수학을 사용해 이 표면의 탄젠트 및 비트 탄젠트 벡터를 수동으로 계산한다.
plane이 다음 벡터들로 구성되었다고 가정하자:
// positions
glm::vec3 pos1(-1.0, 1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3( 1.0, -1.0, 0.0);
glm::vec3 pos4( 1.0, 1.0, 0.0);
// texture coordinates
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// normal vector
glm::vec3 nm(0.0, 0.0, 1.0); 먼저 첫 번째 삼각형의 가장자리와 델타 UV 좌표를 계산한다:
glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1; 탄젠트 및 비트 탄젠트를 계산하는데 필요한 데이터를 사용해 이전 섹션의 방정식을 따라 시작할 수 있다:
float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent1 = glm::normalize(tangent1);
bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent1 = glm::normalize(bitangent1);
[...] // similar procedure for calculating tangent/bitangent for plane's second triangle여기서 우리는 먼저 방정식의 분수 부분을 f로 사전 계산한 다음 각 벡터 성분에 대해 대응하는 행렬 곱셈에 f를 곱한다.
이 코드를 최종 방정식과 비교하면 직접적인 변환임을 알 수 있다. 마지막으로 우리는 탄젠트/비트 탄젠트 벡터가 단위 벡터로
끝나는지 확인하기 위해 정규화를 수행한다.
삼각형은 항상 평면 모양이므로 삼각형의 정점 각각에 대해 동일하므로 삼각형당 하나의 탄젠트/비탄젠트 쌍을 계산하면 된다.
대부분의 구현에는 일반적으로 다른 삼각형과 정점을 공유하는 삼각형이 있다. 이 경우 개발자는 보통 각 꼭지점의 법선 및 탄젠트/비탄젠트와
같은 정점 속성을 평균화해 보다 부드러운 결과를 얻는다. 비행기의 삼각형도 일부 꼭지점을 공유하지만 두 삼각형이 서로 평행하기 때문에
결과를 평균할 필요는 없다. 그러나 이러한 상황에 직면할 때마다 이를 명심하는 것이 좋다.
결과 접선 및 비탄젠트 벡터는 법선 (0,0,1)과 함께 직교 TBN 행렬을 형성하는 각각 (1,0,0) 및 (0,1,0)의 값을 가져야한다.
비행기에서 시각화된 TBN 벡터는 다음과 같다:
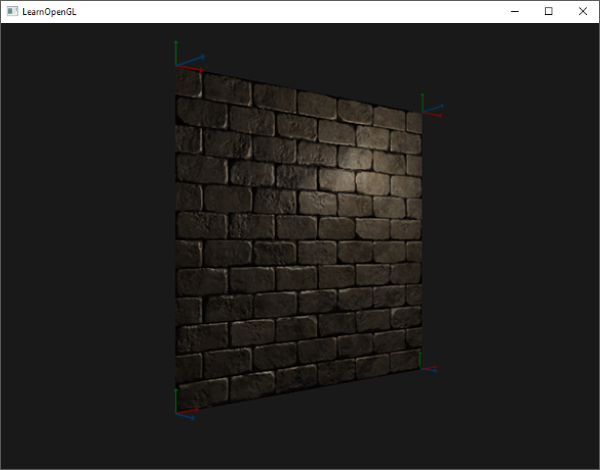
정점마다 정의된 접선 및 비트 탄젠트 벡터를 사용해 적절한 노멀 맵핑을 구현할 수 있다.
Tangent space normal mapping
정상적인 맵핑 작업을 하려면 먼저 쉐이더에 TBN 행렬을 만들어야한다. 이를 위해 이전에 계산된 탄젠트 및 비탄젠트 벡터를
정점 쉐이더에 정점 속성으로 전달한다:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent; 그런 다음 정점 쉐이더의 주요 함수 내에서 TBN 행렬을 만든다:
void main()
{
[...]
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
mat3 TBN = mat3(T, B, N)
}
여기서 우리는 먼저 모든 TBN 벡터를 우리가 작업하고자 하는 좌표계로 변환한다. 이 경우에는 모델 행렬로 곱하면 세계 공간이다.
그런 다음 mat3의 생성자에 관련 벡터를 직접 제공해 실제 TBN 행렬을 만든다. 우리가 정말로 정확하기를 원한다면 TBN 벡터에 모델 행렬을
곱하지 않고, 정규 행렬을 사용하면 translation과 scailing 변환이 아닌 벡터의 방향만 고려하므로 주의해야한다.
이제 우리는 TBN 행렬을 가지게되었다. 어떻게 사용하나? 기본적으로 TBN 행렬을 일반 맵핑에 사용할 수 있는 두 가지 방법이 있으며
두 가지를 모두 보여주겠다.
1. 우리는 모든 벡터를 접선에서 세계 공간으로 변환하고 그것을 조각 쉐이더에 주고 TBN 행렬을 사용해 탄젠트 공간에서
월드 공간으로 샘플된 법선을 변환하는 TBN 행렬을 취한다. 법선은 다른 조명 변수와 동일한 공간에 있다.
2. 우리는 TBN 행렬의 역함수를 취해 모든 벡터를 월드 공간에서 접선 공간으로 변환하고 이 행렬을 사용해 일반이 아닌
다른 관련 조명 변수를 접선 공간으로 변환한다. 법선은 다른 조명 변수와 동일한 공간에서 다시 나타난다.
첫 번째 사례를 살펴보자. 노멀 맵에서 샘플링한 법선 벡터는 접선 공간으로 표현되는 반면 다른 조명 벡터는 월드 공간에서 표현된다.
TBN 행렬을 조각 쉐이더에 전달함으로써 샘플된 접선 공간 법선에 이 TBN 행렬을 곱해 법선 벡터를 다른 조명 벡터와 동일한
참조 공간으로 변환 할 수 있다. 이 방법으로 모든 조명 계산을 이해할 수 있다.
TBN 행렬을 조각 쉐이더에 보내는 것은 쉽다:
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} vs_out;
void main()
{
[...]
vs_out.TBN = mat3(T, B, N);
}조각 쉐이더에서는 입력 변수로 mat3를 사용한다:
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} fs_in; TBN 행렬을 사용하면 일반 맵핑 코드를 업데이트해 전 세계 접선 변환을 포함할 수 있다:
normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);
normal = normalize(fs_in.TBN * normal); 결과로 얻은 법선이 현재 월드 공간에 있기 때문에 조명 코드가 법선 벡터가 월드 공간에 있다고 가정하므로 다른 조각 쉐이더 코드를
변경할 필요가 없다.
두 번째 경우를 검토해보자. TBN 행렬의 역함수를 취해 모든 관련 세계 공간 벡터를 샘플된 벡터가 있는 공간, 즉 접선 공간으로 변환한다.
TBN 행렬의 구조는 동일하게 유지되지만 먼저 행렬을 역 분수 쉐이더로 보내기 전에 이 행렬을 역변환한다:
vs_out.TBN = transpose(mat3(T, B, N)); 여기에서 inverse 함수 대신 transpose 함수를 사용한다. 직교 행렬의 큰 특성은 직교 행렬의 전치가 역행렬과 동일하다는 것이다.
반전은 꽤 비싸고 transpose는 그렇지 않기 때문에 이것은 큰 자산이다. 결과는 같다.
조각 쉐이더 내에서 우리는 법선 벡터를 변형시키지 않지만 다른 관련 벡터를 접선 공간, 즉 lightDir 및 viewDir 벡터로 변환한다.
그런 식으로 각 벡터는 다시 같은 좌표계에 있다: 접선 공간.
void main()
{
vec3 normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);
vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos);
vec3 viewDir = fs_in.TBN * normalize(viewPos - fs_in.FragPos);
[...]
} 두 번째 접근법은 더 많은 작업처럼 보이고 조각 쉐이더에서 더 많은 행렬 곱셈을 요구하는데 왜 두 번째 접근법을 고민하는 걸까?
세계에서 접선 공간으로 벡터를 변형하는 것은 모든 관련 벡터를 조각 쉐이더가 아닌 정점 쉐이더의 접선 공간으로 변환할 수 있다는
장점이 있다. lightPos와 viewPos는 각각의 조각 실행을 변경하지 않고 fs_in.FragPos에 대해 정점 쉐이더의 탄젠트 공간 위치를
계산할 수 있으며 조각 보간 작업을 수행할 수 있다. 기본적으로, 어떤 벡터도 조각 쉐이더의 접선 공간으로 변환 할 필요는 없지만,
첫 번째 접근법으로 샘플링된 법선 벡터는 각 조각 쉐이더 실행에 필요하다.
따라서 TBN 행렬의 역수를 조각 쉐이더에 보내는 대신 접선 공간 라이트 위치, 뷰 위치 및 정점 위치를 조각 쉐이더에 보낸다.
이렇게 하면 조각 쉐이더에서 행렬 곱셈을 줄일 수 있다. 정점 쉐이더가 조각 쉐이더보다 훨씬 덜 자주 실행되기 때문에 좋은 최적화이다.
이것은 또한 이 접근법이 종종 선호되는 접근법인 이유이기도 하다.
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
uniform vec3 lightPos;
uniform vec3 viewPos;
[...]
void main()
{
[...]
mat3 TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vec3(model * vec4(aPos, 0.0));
} 조각 쉐이더에서는 이러한 새로운 입력 변수를 사용해 접선 공간에서 조명을 계산한다. 법선 벡터가 이미 접선 공간에 있으므로
조명이 의미가 있다.
탄젠트 공간에 일반 맵핑을 적용한 경우 이 튜토리얼의 시작 부분에서 얻은 결과와 비슷한 결과를 얻지만 이번에는 원하는 방식으로
평면을 배치 할 수 있으며 조명은 여전히 정확하다:
glm::mat4 model;
model = glm::rotate (model, (float)glfwGetTime () * -10.0f, glm::normalize(glm::vec3(1.0, 0.0, 1.0)));
shader.setMat4("model", model);
RenderQuad();실제로 올바른 노말 맵핑은 다음처럼 보인다:
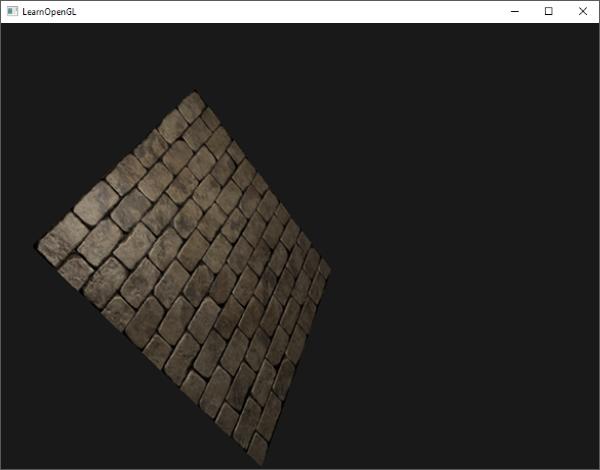
Complex objects
우리는 탄젠트 및 비탄젠트 벡터를 수동으로 계산해 탄젠트 공간 변환과 함께 일반 맵핑을 사용하는 방법을 시연했다.
운 좋게도 우리가 직접 접하는 벡터를 수동으로 계산해야하는 것이 많이 해야할 작업은 아니다. 사용자 정의 모델 로더에서 한 번 구현하거나
Assimp를 사용해 모델 로더를 사용하는 경우가 대부분이다.
Assimp는 aiProcess_CalcTangentSpace라는 모델을 로드 할 때 설정할 수 있는 매우 유용한 구성 비트를 가지고 있다.
Assimp의 ReadFile 함수에 aiProcess_CalcTangentSpace 비트가 제공 될 때 Assimp는 로드된 정점에 대해 매끄러운 탄젠트 및
비탄젠트 벡터를 계산한다. 이 튜토리얼에서의 방법과 유사하다.
const aiScene *scene = importer.ReadFile(
path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace
); Assimp 내에서 다음을 통해 계산된 탄젠트를 검색할 수 있다:
vector.x = mesh->mTangents[i].x;
vector.y = mesh->mTangents[i].y;
vector.z = mesh->mTangents[i].z;
vertex.Tangent = vector; 그런 다음 모델 로더를 업데이트해 텍스처 모델에서 노멀 맵을 로드해야한다. 웨이브 프런트 객체 포맷 (.obj)은 aiTextureType_HEIGHT가
수행하는 동안 Assimp의 aiTextureType_NORMAL이 노멀 맵을 로드하지 않기 때문에 약간 다른 노멀 맵을 내보낸다:
vector<Texture> normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal"); 물론 이것은 로드된 모델 및 파일 형식의 각 유형마다 다르다. 또한, 중요한 것은 aiProcess_CalcTangentSpace가 항상 작동하지 않는다는
것이다. 탄젠트 계산은 텍스처 좌표를 기반으로 하며 일부 모델 아티스트는 텍스처 좌표의 절반을 미러링해 모델 위에 텍스처 표면을
미러링하는 것과 같은 특정 텍스처 트릭을 수행한다. 미러링이 고려되지 않은 경우 잘못된 결과가 나타난다. (Assimp는 그렇지 않다)
예를 들어, nanosuit 모델은 텍스처 좌표를 미러링 했으므로 적절한 탄젠트를 생성하지 않는다.
업데이트된 모델 로더를 사용해 반사 및 법선 맵으로 올바르게 텍스처 매핑된 모델에서 어플리케이션을 실행하면 다음과 같은 결과가 나타난다:

보시다시피 정상적인 맵핑은 너무 많은 추가 비용없이 엄청난 양의 객체 디테일을 향상시킨다.
노멀 맵을 사용하는 것도 장면의 성능을 향상시키는 좋은 방법이다. 노멀 맵핑을 하기 전에 다수의 정점을 사용해 메쉬에 많은 수의 디테일을
표현해야했지만, 노멀 맵핑을 사용하면 훨씬 적은 정점을 사용해 동일한 레벨의 디테일을 메쉬에 표시 할 수 있다.
Paolo Cignoni의 아래 이미지는 두 가지 방법 모두를 비교해보았다:
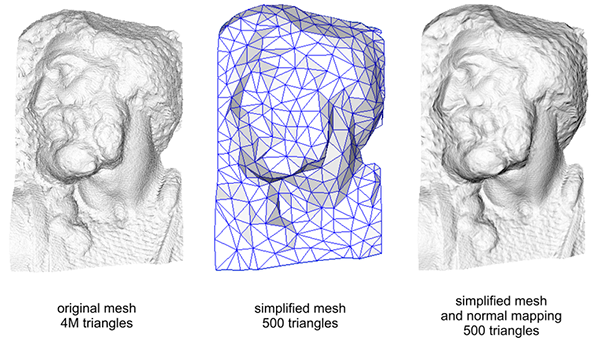
높은 정점 메쉬와 일반 정점 맵핑을 가진 낮은 정점 메쉬의 세부 사항은 거의 구분할 수 없다. 따라서 정상적인 맵핑은 멋지게 보일뿐만
아니라 높은 정점 폴리곤을 낮은 정점 폴리곤으로 대체하는 훌륭한 도구이다.
One last thing
지나치게 많은 추가 비용없이 품질을 약간 향상시키는 일반 맵핑과 관련해 논의하고자 하는 마지막 트릭이 하나 있다.
상당한 양의 정점을 공유하는 더 큰 메쉬에서 탄젠트 벡터를 계산할 때 탄젠트 벡터는 일반적으로 이러한 맵핑이 정상적으로 적용될 때
멋지고 부드러운 결과를 제공하기 위해 평균화된다. 이 접근 방식의 문제점은 3개의 TBN 벡터가 서로 수직이 아니게 되어
결과적으로 TBN 행렬이 더 이상 직각이 아닐 수 있다는 것이다. 정규 맵핑은 비 직교 TBN 행렬을 사용해 약간 벗어나지만
여전히 개선 할 수 있는 부분이다.
Gram-Schmidt(그램-슈미트) 과정이라는 수학적 기법을 사용해 TBN 벡터를 다시 직교화 할 수 있으므로 각 벡터가 다른 벡터와 수직이 된다.
정점 쉐이더 내에서 우리는 이렇게 할 것이다:
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
// re-orthogonalize T with respect to N
T = normalize(T - dot(T, N) * N);
// then retrieve perpendicular vector B with the cross product of T and N
vec3 B = cross(N, T);
mat3 TBN = mat3(T, B, N) 이것은 약간은 아니지만 일반적으로 약간의 추가 비용으로 정상적인 맵핑 결과를 향상시킨다. 이 과정이 실제로 어떻게 작동하는지에
대한 훌륭한 설명을 원한다면 이 튜토리얼 아래에서 언급한 Normal Mapping Mathematics 비디오의 끝 부분을 살펴보아라.
'Game > Graphics' 카테고리의 다른 글
| LearnOpenGL - Advanced Lighting : HDR (0) | 2018.10.03 |
|---|---|
| LearnOpenGL - Advanced Lighting : Parallax Mapping (0) | 2018.10.02 |
| Learn OpenGL - Advanced Lighting : Point Shadows (2) (0) | 2018.10.01 |
| Learn OpenGL - Advanced Lighting : Point Shadows (1) (0) | 2018.09.27 |
| Learn OpenGL - Advanced Lighting : Shadow Mapping (3) (0) | 2018.09.27 |






