link : https://learnopengl.com/Getting-started/Transformations
Transformations
우리는 이제 오브젝트를 생성하고, 색상을 지정하고, 텍스처를 사용해 자세한 모양을 제공하는 방법을 알고 있다.
그러나 그것들은 모두 정적 오브젝트이므로 여전히 흥미롭지 않다.
정점을 변경하고 각 프레임의 버퍼를 다시 구성해 시도해 볼수는 있지만 성가시고 비용이 많이 든다.
객체를 변형하는 방법은 훨씬 더 많다. 그 방법은 (여러) 행렬 객체를 사용하는 것이다.
이것은 우리가 kungfu 및 큰 디지털 인공 세계에 대해서 이야기하기 위해 하고 있다는 것을 의미하지 않는다.
행렬은 처음에는 두려운 것처럼 보이는 매우 강력한 수학적 구조이지만 일단 익숙해지면 매우 유용한다.
행렬에 대해 논의할 때 우리는 약간의 수학에 잠깐 들어가야 할 것이며, 더 수학적으로 관심이 있는 독자들을
위해 추가 읽기를 위한 추가 자료를 게시할 것이다.
그러나 변환을 완전히 이해하려면 먼저 행렬을 논의하기 전에 벡터에 대해 좀 더 깊이 파고 들어야한다.
이 장의 초점은 나중에 필요할 주제에 대한 기본적인 수학적 배경을 제공하는 것이다.
주제가 어려울 경우 가능한 많이 이해하고 이 페이지로 돌아와 필요할 때마다 개념을 검토해라.
Vectors
가장 기본적인 정의에서 벡터는 방향과 그 이상이다. 벡터는 방향과 크기를 가진다. (강도 또는 길이라고도 함)
보물지도에서 방향과 같은 벡터를 생각할 수 있다. '왼쪽으로 10걸음, 북쪽으로 3걸음, 오른쪽으로 5걸음';
여기서 '왼쪽'은 방향이고 '10걸음'은 벡터의 크기이다. 따라서 보물지도의 지시에는 3개의 벡터가 포함된다.
벡터는 임의의 차원을 가질 수 있지만 일반적으로 2차원에서 4차원까지 작업한다.
벡터가 2차원인경우 벡터는 평면상의 방향을 나타내며 (2D 그래프를 생각할 때) 3차원을 가지면 3D에서 모든 방향을 나타낼 수 있다.
아래에서 3개의 벡터를 볼 수 있다. 각 벡터는 2D 그래프의 화살표로 (x,y)로 표시된다. 벡터를 2D로 표시하는 것이 3D보다 더 직관적이므로
2D 벡터를 z 좌표가 0인 3D 벡터로 생각할 수 있다. 벡터는 방향을 나타내므로 벡터의 원점은 값을 변경하지 않는다.
아래의 그래프에서 벡터 v와 w는 원점이 다르더라도 동일하다는 것을 알 수 있다:
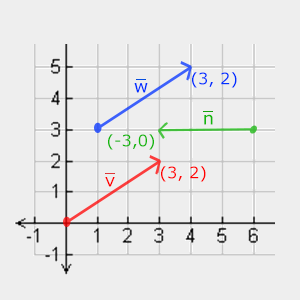
벡터를 기술 할 때 수학자들은 일반적으로 벡터를 v와 같이 머리 위에 작은 막대가 있는 문자 기호로 설명하는 것을 선호한다.
또한, 수식에 벡터를 표시할 때 일반적으로 다음과 같이 벡터가 표시된다.
벡터는 방향으로 지정되기 때문에 위치로 시각화하는 것이 때때로 어렵다. 우리가 기본적으로 시각화 한 것은 방향의 원점을 (0,0,0) 으로 설정한
다음 점을 지정하는 특정 방향을 가리키고 위치 벡터로 만든다. 그러면 위치 벡터 (3,5)는 원점이 (0,0)인 그래프에서 (3,5)를 가리킨다.
벡터를 사용해 2D 및 3D 공간에서 방향과 위치를 설명할 수 있다.
일반 숫자와 마찬가지로 벡터에 대한 연산도 정의할 수 있다.
Scalar vector operations
스칼라는 한자리 수이다. 벡터를 스칼라로 더하기/빼기/곱하기 또는 나눌 때 벡터의 각 요소를 스칼라로 연산하면 된다.
추가로 다음과 같이 보인다:
Vector negation
벡터를 음수로 지정하면 반대 방향으로 벡터가 된다. 북동쪽을 가리키는 벡터는 부정을 한 후 남서쪽을 가리킬 것이다.
벡터를 무효화하려면 각 구성 요소에 빼기 부호를 추가해라.
Addition and subtraction
두 벡터의 합을 하나의 벡터의 각 구성 요소가 다른 벡터의 동일한 구성 요소에 다음과 같이 추가되는 구성 요소 별
추가로 정의된다:
시각적으로 벡터 v = (4,2)와 k = (1,2)에서 다음과 같이 보인다.
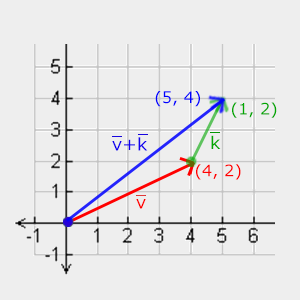
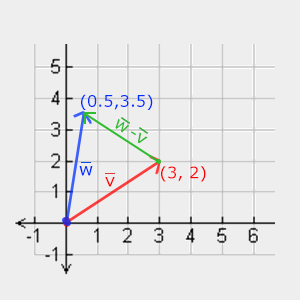
정상적인 더하기 및 빼기와 마찬가지로 벡터 빼기는 네거티브된 두 번째 벡터가 있는 덧셈과 같다.
두 벡터를 빼면 두 벡터가 가리키는 위치의 차이인 벡터가 된다. 이것은 두 가지 점의 차이인 벡터를 검색해야하는 경우에 유용하다.
Length
벡터의 길이/크기를 검색하기 위해 수학 수업에서 기억할 수 있는 피타고라스 정리를 사용한다. 개별 x 및 y 구성 요소를 삼각형의
두 면으로 시각화해 벡터가 삼각형을 형성한다.
||v-|| 는 벡터 v-의 길이로 표시된다. 이것은 z^2를 방정식에 추가해 3D롤 쉽게 확장된다.
이 경우 벡터 (4,2)의 길이는 다음과 같다:
4.47이다.
우리가 단위 벡터라고 부르는 특별한 유형의 벡터도 존재한다. 단위 벡터는 하나의 여분 속성을 가지며 그 길이가 정확히 1이다.
벡터의 각 구성 요소를 길이로 나눠서 벡터에서 단위 벡터 n을 계산할 수 있다.
이것을 정규화 벡터라고 부른다. 단위 벡터는 머리 위에 약간의 지붕으로 표시되며 일반적으로 다루기가 더 쉽다.
Vector-vector multiplication
두 벡터를 곱하는 것은 다소 이상한 경우이다. 일반 곱셈은 시각적인 의미가 없으므로 벡터에 실제로 정의되어 있지는 않지만
곱셈을 할 때 선택할 수 있는 두 가지 특수한 경우가 있다. 하나는 v- X k- 로 표시되는 내적이고, 다른 하나는 v- x k-이다.
Dot product
두 벡터의 내적은 길이의 스칼라 곱과 그것들 사이의 각의 코사인을 곱한 값과 같다. 이것이 혼란스럽게 들리는 경우 공식을 살펴보아라.
여기서 그 사이의 각도는 세타(θ)로 표시된다.
이제 내적은 두 벡터 사이의 각도만 정의한다. cosine or cos함수는 각도가 90도 일 때 0이되거나 각도가 0 일 때 1이 된다는 것을 기억할 것이다.
이렇게하면 두 벡터가 내적을 사용해 서로 직각 또는 평행한지 쉽게 테스트할 수 있다.
그렇다면 우리는 어떻게 내적을 계산할까? 내적은 결과를 함께 더하는 구성 요소별 곱셈이다. 이것은 두 개의 단위 벡터로 보인다.
이 두 단위 벡터 사이의 차수를 계산하기 위해 우리는 코사인 함수 cos^-1의 역함수를 사용하며 이 결과는 143.1도이다. 우리는 이 두 벡터 사이의
각도를 효과적으로 계산했다. 내적 계산은 조명 계산을 수행할 때 매우 유용하다.
Cross product
교차 곱은 3D 공간에서만 정의되며 두 개의 비평행 벡터를 입력으로 사용하고 두 입력 벡터와 직교하는 세 번째 벡터를 생성한다.
두 입력 벡터가 서로 직교하더라도 교차 곱은 3개의 직교 벡터가 된다. 이것은 곧 나오는 튜토리얼에서 유용할 것이다.
다음 이미지는 3D 공간에서 이 모양을 보여준다.
다른 연산과 달리 교차 곱은 선형 대수학을 탐구하지 않으면 직관적이지 않으므로 수식을 외워 두는 것이 좋다. 아래에서 두 개의 직교
벡터 A와 B사이의 외적을 볼 수 있다.
보시다시피 실제로는 의미가 없는 것처럼 보인다. 그러나 이러한 단계를 수행하면 입력 벡터와 직각을 이루는 다른 벡터가 생긴다.
Matrices
벡터에 대한 거의 모든 것이 논의되었으므로 매트릭스에 들어갈 시간이다. 행렬은 기본적으로 숫자, 기호와 또는 표현식의 직사각형 배열이다.
행렬의 각 개별 항목을 행렬의 요소라고 한다. 2x3 행렬의 예가 아래에 나와 있다.
행렬은 (i,j)에 의해 인덱싱된다. 여기서 i는 행이고 j는 열이다. 따라서 위의 행렬은 2x3 행렬 (3열 2행, 행렬의 차원이라고도 함)이라고 한다.
이는 2D 그래프를 (x, y)로 인덱싱 할 때 익숙한 것과 반대이다. 값 4를 검색하려면 값을 (2,1)로 인덱싱한다.
행렬은 기본적으로 수학 표현식의 사각형 배열이다. 그것들은 매우 훌륭한 수학적 속성 집합을 가지고 있으며 벡터와 마찬가지로
행렬에 대한 여러 연산 즉, 더하기, 빼기 및 곱셈을 정의할 수 있다.
Scailing
벡터 크기를 조절할 때 우리는 방향을 동일하게 유지하면서 크기를 조정하려는 양만큼 화살표의 길이를 늘립니다.
우리는 2차원 또는 3차원으로 작업하기 때문에 2개 또는 3개의 스케일링 변수의 벡터로 스케일링을 정의할 수 있다.
각 스케일링은 하나의 축 (x,y 또는 z)을 스케일한다.
벡터를 스케일링해보자. v = (3,2). 우리는 벡터를 x축을 따라 0.5만큼 스케일링 할 것이고, 따라서 그것을 두 배로 좁힐 것이다.
y축을 따라 벡터를 2로 스케일링해 두 배로 스케일링한다. 벡터를 (0.5, 2)로 스케일링하면 어떻게 생겼는지 보자.
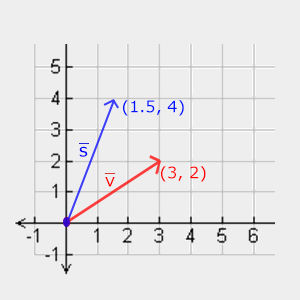
OpenGL은 일반적으로 3D 공간에서 작동하므로 2D 케이스의 경우 z축 스케일을 1로 설정해 무사히 유지할 수 있다.
스케일링 팩터가 각 축에 동일하지 않기 때문에 방금 수행한 스케일링 연산은 비 균일 스케일이다. 스칼라가 모든 축에서 동일하면
일정한 스케일이라고 한다.
우리를 위한 스케일링을 수행하는 변형 행렬을 작성해보자. 우리는 항등 행렬로부터 각 대각 요소가 대응하는 벡터 요소와
곱해지는 것을 보았다. 단위 행렬의 1을 3으로 변경하면 어떨까? 이 경우 각 벡터 요소에 3을 곱해 벡터를 3으로 효과적으로 스케일한다.
스케일링 변수를 (S1, S2, S3)로 표현하면 모든 벡터에서 스케일링 행렬을 정의할 수 있다. (x,y,z)
3D 공간에서 w 구성 요소의 크기를 조정하는 것은 정의되지 않았기 때문에 4번째 배율 벡터는 1로 유지된다. w 컴포넌트는 나중에 보게 될 다른
목적으로 사용된다.
Translation
번역이란 원본 벡터 위에 다른 벡터를 추가해 다른 위치의 새 벡터를 반환해 번역 벡터에 따라 벡터를 이동하는 프로세스이다.
우리는 이미 벡터 추가에 대해 논의했으므로 너무 새롭지 않아야한다.
스케일링 행렬과 마찬가지로 특정 연산을 수행하는데 사용할 수 있는 4x4 매트릭스의 여러 위치가 있으며 변환을 위해서는 4x 째 컬럼의
최상위 3값이 있다. 스케일링 벡터를 (Tx, Ty, Tz)로 나타내면 다음과 같이 변환 행렬을 정의할 수 있다.
이 작업은 모든 변환 값에 벡터의 w열을 곱하고 벡터의 원래 값에 더하기 때문에 작동한다. 이것은 3x3 매트릭스로는 불가능 했을 것이다.
벡터의 w 구성 요소는 homogeneous 좌표라고도 한다. 호모지니어스 벡터로부터 3D 벡터를 얻으려면 x, y 및 z 좌표를 w 좌표로 나눈다. w 요소는 대부분 1.0이므로 이 사실을 알 수 없다. 동질적인 좌표를 사용하면 몇 가지 이점이 있다. 즉, 벡터를 변환할 수 없는 w 요소 없이 3D 벡터에 대한 변환을 수행할 수 있으며 다음 장에서는 w값을 사용해 3D 비주얼을 생성한다.
또한 동질 좌표가 0일 때마다 w좌표가 0인 벡터를 변환할 수 없으므로 벡터를 방향 벡터라고 한다.
변환 행렬을 사용해 우리가 원하는 3가지 방향 (x,y,z)으로 객체를 이동할 수 있으므로 변형 툴킷에 매우 유용한 변형 행렬이 된다.
Rotation
지난 몇 변의 변형은 2D 또는 3D 공간에서 비교적 쉽게 이해하고 시각화 할 수 있었지만 회전은 조금 까다롭다.
이 매트릭스가 어떻게 구성되었는지 정확히 알고 싶다면 Khan Academy의 선형 대수학 비디오의 rotation 항목을 보는 것이 좋다.
먼저 벡터의 회전이 실제로 무엇인지 정의해보자. 2D 또는 3D 회전은 각도로 표시된다. 각도는 degree 혹은 radian으로 표시할 수 있으며
전체 원은 360도 또는 2 PI 라디안이다.
angle in degrees = angle in radians * (180.0f / PI)
angle in radians = angle in degrees * (PI / 180.0f)
PI = 3.14159265359
반원을 돌리면 360 / 2 = 180도 회전하고 1 / 5 회전하면 오른쪽으로 360 / 5 = 72도 회전한다. 이것은 v-가 k에서 오른쪽으로 72도 회전된
기본 2D 벡터에 대해 설명된다.
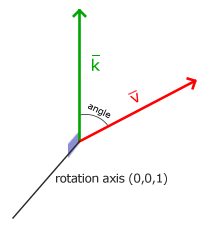
3D에서의 회전은 각도와 회전 축으로 지정된다. 지정된 각도는 지정된 회전 축을 따라 객체를 회전시킨다. 하나의 회전 축을 계속 보면서
머리를 어느 정도 회전시켜 시각화해라. 예를 들어 3D 세계에서 2D 벡터를 회전시킬 때 회전 축을 z축으로 설정한다.
삼각법을 사용하면 각도를 부여한 새로운 회전 벡터로 벡터를 변환할 수 있다. 이것은 일반적으로 사인 함수와 코사인 함수의 스마트 조합을 통해
수행된다. 변환 행렬 생성 방법에 대한 설명은 이 튜토리얼의 범위를 벗어난다.
각도가 θ 기호로 표시되는 3D 공간에서 각 단위 축에 대해 회전 행렬이 정의된다.
Rotation around the X-axis:
Rotation around the Y-axis:
Rotation around Z-axis:
회전 행렬을 사용해 3개의 단위 축 중 하나에 위치 벡터를 변형할 수 있다. X축과 Y축을 중심으로 회전시켜 결합할 수도 있다. 그러나 이것은 Gimbal lock이라는
문제를 신속하게 발생시킨다. 세부 사항은 다루지 않지만 더 나은 해결책은 임의의 단위 축을 기준으로 회전하는 것이다.
(0.662, 0.2, 0.722) (이것은 단위 벡터임을 유의해라) 회전 행렬을 결합하는 대신에 바로 그런 행렬이 존재하며 아래에 임의의 축으로 (Rx, Ry, Rz)가 주어진다:
그러한 행렬을 생성하는 수학적 논의는 이 튜토리얼의 범위를 벗어난다. 이 매트릭스조차도 짐벌 잠금을 완전히 막지는 못한다는 사실을 명심해라.
회전은 쿼터니언을 사용하면 더 안전할 뿐만 아니라 더 계산상 친숙하다. 그러나 쿼터니언에 대한 설명은 나중에 자습서를 위해 예약되어 있다.
Combining matrices
변환을 위한 행렬 사용의 진정한 힘은 행렬-행렬 곱셈 덕분에 단일 행렬에서 여러 변환을 결합할 수 있다는 것이다. 여러 변형을 결합한
변형 행렬을 생성할 수 있는지 보자. 벡터 (x, y, z)가 있고 그것을 2로 스케일한 후 (1,2,3)로 변환하고 싶다고 하자. 우리는 필요한 단계를 위해
번역 및 스케일링 매트릭스가 필요하다. 결과 변환 행렬은 다음과 같다.
먼저 행렬을 곱할 때 변환을 수행한 다음 스케일 변환을 수행한다. 행렬 곱셈은 교환이 가능하지 않으므로 순서가 중요하다.
행렬을 곱할때 맨 오른쪽 행렬이 먼저 벡터에 곱해져서 오른쪽에서 왼쪽으로 곱셈을 읽어야한다. 먼저 스케일링 연산을 수행한 다음 행렬을 결합할 때
회전과 마지막으로 변환을 수행하는 것이 좋다. 그렇지 않으면 서로 영향을 미칠 수 있다. 예를 들어, 먼저 translation을 수행한 다음 비율을 조정하면
translation 벡터도 확장된다.
벡터에서 최종 변형 행렬을 실행하면 다음 벡터가 생성된다.
Great! 벡터는 2로 스케일 된 다음 (1,2,3)으로 translate된다.
In practice
이제 우리는 변환의 모든 이론을 설명했으므로, 실제로 이 지식을 우리의 이점에 어떻게 활용할 수 있는지
알아보아야할 때이다. OpenGL은 어떤 형태의 행렬 또는 벡터 지식도 내장하고 있지 않으므로 우리는 우리 자신의
수학 클래스와 함수를 정의해야한다. 튜토리얼에서 우리는 모든 작은 수학적 세부 사항을 추상화하고
미리 만들어진 수학 라이브러리를 사용한다. 다행히 GLM이라는 OpenGL 수학 라이브러리가 사용하기 쉽고
맞춤형이다.
GLM
GLM은 OpenGL Mathematics의 약자이며 헤더 전용 라이브러리이다. 즉, 적절한 헤더 파일만 포함하면된다.
연결 및 컴파일이 필요없다. GLM은 [https://glm.g-truc.net/0.9.8/index.html]에서 다운로드 할 수 있다.
헤더 파일의 루트 디렉토리를 include 폴더에 복사하고 롤링을 시작한다.
우리가 필요로 하는 대부분의 GLM 기능은 다음과 같이 포함시킬 3개의 헤더 파일에서만 찾을 수 있다.
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>(1, 0, 0)의 벡터를 (1, 1, 0)으로 변환해 변환 지식을 잘 활용 할 수 있는지 보자 (glm::vec4로 정의함):
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans;
trans = glm::translate (trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;먼저 GLM에 내장된 벡터 클래스를 사용해 vec라는 벡터를 정의한다. 다음 단계는 우리의 단위 행렬을 translate 벡터와 함께
glm::translate 함수에 전달해 변환 행렬을 생성하는 것이다. (주어진 행렬에 변환 행렬을 곱한 결과 행렬을 반환)
그런 다음 우리 벡터에 변환 행렬을 곱해 결과를 출력합니다. 우리가 여전히 행렬 변환이 작동하는 방법을 기억한다면 결과 벡터는
(1 + 1, 0 + 1, 0 + 0)이 되어야한다. (2, 1, 0). 이 코드의 스니펫은 210을 출력해 translate 행렬이 작업을 수행하는 것을 알 수 있다.
좀 더 흥미롭게 이전 튜토리얼의 컨테이너 오브젝트를 scale하고 rotate 해보자:
glm::mat4 trans;
trans = glm::rotate (trans, glm::radians (90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale (trans, glm::vec3(0.5, 0.5, 0.5)); 먼저 각 축에서 컨테이너를 0.5만큼 스케일 한 다음 컨테이너를 Z 축을 중심으로 90도 회전시킨다.
GLM은 라디안으로 그 각도를 예상하므로 glm::radians를 사용해 degree를 radian으로 변환한다.
텍스처 사각형은 XY 평면상에 있으므로 Z축을 중심으로 회전하고 싶다. 회전하는 축은 단위 벡터여야하므로 X, Y 또는
Z축을 중심으로 회전하지 않는 경우 먼저 벡터를 정규화해야한다. 행렬을 GLM의 각 함수에 전달하기 때문에 GLM은
행렬을 자동으로 곱해 모든 변환을 결합하는 변환 행렬을 만든다.
다음으로 중요한 질문은 transformation 행렬을 쉐이더에 어떻게 적용할까? GLSL은 또한 mat4 타입을 가지고 있다는 것을
전에 간단히 언급했다. 그래서 우리는 mat4 균일 변수를 받아들이도록 정점 쉐이더를 적용하고 위치 벡터에 행렬
유니폼을 곱한다:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
TexCoord = vec2(aTexCoord.x, aTexCoord.y);
} 우리는 uniform을 더하고 gl_position에 전달하기 전에 위치벡터에 변환 행렬을 곱했다.
우리 컨테이너는 이제 두 배로 작아져야하고 90도 회전한다. (왼쪽으로 기울어짐)
그래도 transformation 행렬을 쉐이더에 전달해야한다:
unsigned int transformLoc = glGetUniformLocation (ourShader.ID, "transform");
glUniform Matrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));먼저 uniform 변수의 위치를 쿼리한 다음 행렬 데이터를 Matrix4fv를 후위로 사용해 glUniform 함수를 통해
쉐이더에 보낸다.
첫 번째 인수는 지금까지는 유니폼의 위치에 익숙해야한다. 두 번째 인수는 OpenGL에 전달하고자 하는 행렬의 수를 1로 지정한다.
세 번째 인수는 행렬을 swap 할 때 행과 열을 바꿔야 하는지 묻는다.
OpenGL 개발자는 GLM의 기본 행렬 레이아웃인 열 주요 정렬이라고 하는 내부 행렬 레이아웃을 사용하므로 행렬을
조 변경할 필요가 없다. 우리는 그것을 GL_FALSE로 유지할 수 있다. 마지막 인수는 실제 행렬 데이터이다.
그러나 GLM은 행렬을 OpenGL에서 수신하기를 원하는 방식으로 행렬을 저장하지 않으므로 먼저 GLM의 내장함수 value_ptr로 변환한다.
변형 행렬을 생성하고 정점 쉐이더에서 유니폼을 선언하고 행렬을 정점 좌표를 변형시키는 쉐이더로 보냈다.
결과는 다음과 같아야한다.
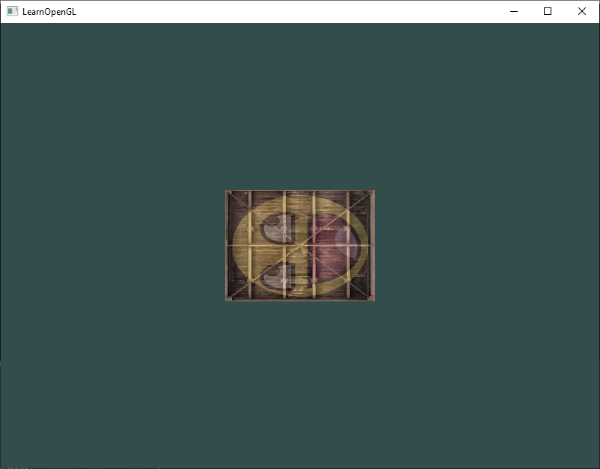
완벽하다! 우리의 컨테이너는 실제로 왼쪽으로 그리고 두 배 작아진 변형이 성공적으로 이루어졌따. 좀 더 펑키하고
시간이 지남에 따라 컨테이너를 회전시킬 수 있는지 살펴보도록하겠다. 재밌게도 window의 오른쪽 하단에 컨테이너의
위치를 재지정한다. 시간이 지남에 따라 컨테이너를 회전하려면 각 반복 반복을 업데이트해야하기 때문에 게임 루프에서
변환 행렬을 업데이트해야한다. GLFW의 시간 함수를 사용해 시간 경과에 따라 약간의 각도를 얻는다:
glm::mat4 trans;
trans = glm::translate (trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate (trans, (float)glfwGetTime (), glm::vec3(0.0f, 0.0f, 1.0f));이전의 경우 변환 행렬을 어디에서나 선언할 수 있었지만 지금은 반복할 때마다 반복 행렬을 만들어야만 한다는 것을 명심해라.
이것은 게임 루프의 반복마다 변환 행렬을 다시 만들어야 함을 의미한다. 일반적으로 장면을 렌더링 할 때 우리는 각각의 반복을
새로운 값으로 재작성한 여러 변환 매트릭스를 가지고 있다.
여기에서는 먼저 컨테이너를 원점 (0,0,0)을 중심으로 회전시키고, 일단 회전하면 회전된 버전을 화면의 오른쪽 하단으로 변환한다.
실제 변환 순서는 역순으로 읽어야한다. 코드에서 처음 변환한 다음 나중에 회전하더라도 실제 변환은 먼저 회전을 적용한 다음
변환을 적용한다. 이러한 모든 변환 조합을 이해하고 오브젝트에 적용하는 방법을 이해하는 것은 어렵다. 이와 같은 변형을 시도해보고
실험하면 빨리 파악할 수 있다. 당신이 일을 제대로 했다면 다음과 같은 결과를 얻어야한다:
시간이 지남에 따라 회전되는 변환된 컨테이너 모두가 단일 변환 행렬에 의해 수행된다!
이제 매트릭스가 그래픽 영역에서 왜 그렇게 강력한 구조인지를 알 수 있다. 우리는 무한한 양의 변환을 정의할 수 있으며,
모든 것을 단일 행렬에 결합해 우리가 원하는만큼 자주 재사용할 수 있다. 정점 쉐이더에서 이와 같은 변형을 사용하면
정점 데이터를 다시 정의하는 노력을 줄일 수 있고, 데이터 처리 시간을 절약할 수 있다.
(데이터를 항상 다시 보내지 않아도 되기 때문에) (but 매우 느리다)
** ** ** ** ** ** ** ** ** **
이번 부분은 학교 컴퓨터 그래픽스 강의에서 배웠던 내용들이 많아서 쉽게 이해할 수 있었다.
기초적인 단순 행렬 사칙연산 부분은 생략했다. 다음 강의부터는 3D 그래픽에 대한 첫 걸음이라고 하니 기대를 가져본다!
'Game > Graphics' 카테고리의 다른 글
| Learn OpenGL - Getting started : Camera (0) | 2018.08.12 |
|---|---|
| Learn OpenGL - Getting started : Coordinate Systems (0) | 2018.08.10 |
| Learn OpenGL - Getting started : Textures (0) | 2018.08.06 |
| Learn OpenGL - Getting started : Shaders (0) | 2018.08.04 |
| Learn OpenGL - Getting started : Hello Triangle (0) | 2018.08.03 |




















