link : https://learnopengl.com/Advanced-OpenGL/Geometry-Shader
Geometry Shader
정점과 조각 쉐이더 사이에 기하학 쉐이더라고 불리는 선택적인 쉐이더 스테이지가 있다. 기하학 쉐이더는 하나의 기본 점 또는 삼각형을
형성하는 정점 세트를 입력으로 사용한다. 그런 다음 기하학 쉐이더는 다음 쉐이더 단계로 보내기 전에 적합하다고 판단되는 대로 이 정점을
변형 할 수 있다. 그러나 기하학 쉐이더를 흥미롭게 만드는 것은 처음에 주어진 것보다 훨씬 많은 정점을 생성 할 수 있는 완전히 다른
프리미티브로 정점 세트를 변환 할 수 있다.
우리는 여러분에게 기하학 쉐이더 예제를 보여줌으로써 여러분을 깊은 곳으로 던질 것이다:
#version 330 core
layout (points) in;
layout (line_strip, max_vertices = 2) out;
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
} 모든 기하학 쉐이더가 시작될 때 우리가 정점 쉐이더로부터 받는 프리미티브 입력의 타입을 선언해야한다. in 키워드 앞에 레이아웃
지정자를 선언해 이 작업을 수행한다. 이 입력 레이아웃 한정자는 정점 쉐이더에서 다음 기본값 중 하나를 취할 수 있다.
1) points : GL_POINTS 를 그릴 때 (1)
2) lines : GL_LINES 또는 GL_LINE_STRIP 을 그릴 때 (2)
3) lines_adjacency : GL_LINES_ADJACENCY 또는 GL_LINE_STRIP_ADJACENCY 를 그릴 때 (4)
4) triangles : GL_TRIANGLES, GL_TRIANGLES_STRIP 또는 GL_TRIANGLE_FAN 을 그릴 때 (3)
5) triangles_adjacency : GL_TRIANGLES_ADJACENCY 또는 GL_TRIANGLE_STRIP_ADJACENCY 를 그릴 때 (6)
이것들은 glDrawArrays와 같은 레더링 호출에 제공 할 수 있는 거의 모든 렌더링 기본 요소이다. 정점을 GL_TRIANGLES로 그리기로
했다면 입력 한정자를 삼각형으로 설정해야한다. 괄호 안의 숫자는 단일 기본 요소에 포함된 최소 정점수를 나타낸다.
그런 다음 기하학 쉐이더가 실제로 출력 할 기본 유형을 지정해야하며 out 키워드 앞에 레이아웃 지정자를 통해 이를 수행한다.
입력 레이아웃 한정자와 마찬가지로 출력 레이아웃 한정자도 여러가지 기본 값을 사용할 수 있다:
- points
- line_strip
- triangles_strip
이 3가지 출력 지정자만 있으면 입력 프리미티브에서 원하는 모양을 거의 만들 수 있다. 예를 들어, 단일 삼각형을 생성하려면
trinagle_strip을 출력으로 지정한 다음 3개의 꼭지점을 출력한다.
기하학 쉐이더는 또한 우리가 출력하는 정점의 최대 개수를 설정할 것을 기대한다. (이 개수를 초과하면 여분의 정점은 그려지지 않는다)
또한, out 키워드의 레이아웃 한정자 내에서 수행할 수 있다. 이 특별한 경우에는 최대 2개의 정점을 가진 line_strip을 출력 할 것이다.
라인 스트립이 무엇인지 궁금한 경우 : line strip은 최소 2포인트를 사용해 한 세트의 포인트를 묶어 하나의 연속 라인을 형성한다.
렌더링 호출에 주어진 각 추가 점은 새 점과 이전 점 사이에 새로운 선을 만든다. 아래 그림에서 우리는 5점의 꼭지점이 있는 이미지를
볼 수 있다:
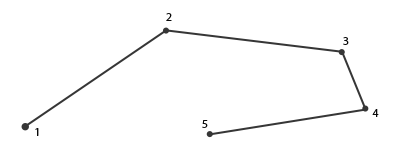
현재 쉐이더에서 최대 정점 수는 2이므로 단 한 줄만 출력한다.
의미있는 결과를 얻으려면 이전 쉐이더 스테이지에서 출력을 검색 할 수 있는 방법이 필요하다. GLSL은 내부적으로 다음과 같은 gl_in이라는
기본 변수를 제공한다:
in gl_Vertex
{
vec4 gl_Position;
float gl_PointSize;
float gl_ClipDistance[];
} gl_in[]; 여기서는 이전 튜토리얼에서 논의한 인터페이스 블록으로 선언된다. 이 인터페이스에는 가장 흥미로운 것이 gl_position이고,
여기에는 정점 쉐이더의 출력으로 설정한 비슷한 벡터가 포함되어 있다.
대부분의 렌더링 프리미티브는 두 개 이상의 꼭지점으로 구성되며 기하학 쉐이더는 프리미티브의 모든 꼭지점을 입력으로 받기 때문에
배열로 선언된다.
이전 정점 쉐이더 단계의 정점 데이터를 사용해 EmitVertex 및 EndPrimitive라는 2개의 쉐이더 함수를 통해 새로운 데이터를 생성 할 수 있다.
기하학 쉐이더는 출력으로 지정한 프리미티브 중 적어도 하나를 생성/출력 할 것을 기대한다. 우리의 경우 최소한 하나의 line strip primitive를
생성하고 싶다:
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
} EmitVertex를 호출 할 때마다 현재 gl_Position으로 설정된 벡터가 프리미티브에 추가된다. EndPrimitive가 호출 될 때 마다 이 프리미티브에
대해 방출된 모든 정점이 지정된 출력 렌더 프리미티브로 결합된다. 하나 이상의 EmitVertex 호출 후에 EndPrimitive를 반복적으로 호출하면
여러 프리미티브를 생성 할 수 있다. 이 특별한 경우는 원래 정점 위치에서 작은 오프셋으로 변환된 두 개의 정점을 방출한 다음
EndPrimitive를 호출해 이 두 정점을 두 정점의 single line strip으로 결합한다.
이제 여러분은 기하학 쉐이더가 어떻게 작동하는지 알게 되었다. 아마도 이 기하학 쉐이더가 무엇을 하는지 짐작할 수 있을 것이다.
이 기하학 쉐이더는 point 프리미티브를 입력으로 사용해 입력 점이 가운데에 있는 가로 선 프리미티브를 만든다.
우리가 이것을 렌더링한다면 다음과 같이 보일 것이다:
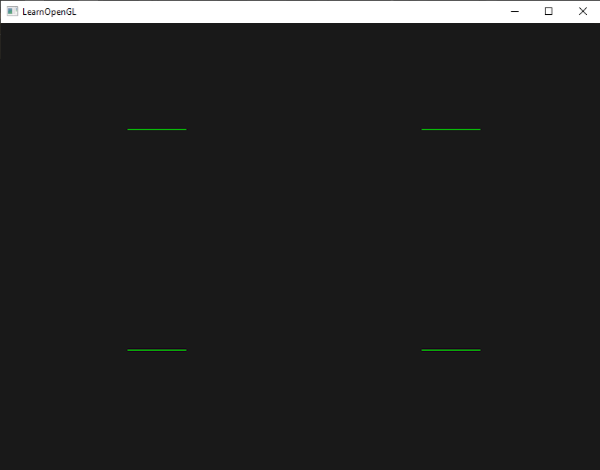
아직 그리 인상적이지는 않지만 다음 출력 호출을 사용해 이 출력이 생성되었다고 생각하는 것은 흥미롭다:
glDrawArrays (GL_POINTS, 0, 4); 이것은 비교적 간단한 예제이지만 기하학 쉐이더를 사용해 동적으로 새로운 shape를 생성하는 방법을 보여준다.
이 튜토리얼의 뒷부분에서 기하학 쉐이더를 사용해 얻을 수 있는 흥미로운 효과에 대해 설명하겠지만,
지금은 간단한 기하학 쉐이더를 만드는 것으로 시작하겠다.
Using geometry shaders
기하학 쉐이더의 사용법을 보여주기 위해 우리는 정규화된 장치 좌표에서 z-평면에 4개의 점을 그려주는 아주 간단한 장면을 렌더링한다.
포인트의 좌표는 다음과 같다:
float points[] = {
-0.5f, 0.5f, // top-left
0.5f, 0.5f, // top-right
0.5f, -0.5f, // bottom-right
-0.5f, -0.5f // bottom-left
}; 정점 쉐이더는 z-평면에 점을 그리기만 하면 되므로 기본 정점 쉐이더만 있으면 된다:
#version 330 core
layout (location = 0) in vec2 aPos;
void main()
{
gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0);
}그리고 조각 쉐이더에서 하드 코드한 모든 포인트에 대해 녹색을 출력한다:
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(0.0, 1.0, 0.0, 1.0);
} 점의 정점 데이터에 대한 VAO와 VBO를 생성한 다음 glDrawArrays를 통해 그린다:
하지만 우리는 이미 이 모든 것을 배우지 않았었나? 이제 장면에 기하학 쉐이더를 추가해 이 작은 장면을 위로 향하게 할 것이다.
학습 목적으로 포인트 프리미티브를 입력으로 사용해 수정되지 않은 다음 쉐이더로 전달하는 pass-through 기하학 쉐이더를 만든다:
#version 330 core
layout (points) in;
layout (points, max_vertices = 1) out;
void main() {
gl_Position = gl_in[0].gl_Position;
EmitVertex();
EndPrimitive();
} 이제 이 기하학 쉐이더는 이해하기 쉽다. 단순히 입력으로 받은 수정되지 않은 정점 위치를 방출하고 점 기본형을 생성한다.
기하학 쉐이더는 정점 및 조각 쉐이더처럼 컴파일하고 프로그램에 링크해야 하지만 이번에는 GL_GEOMETRY_SHADER를 쉐이더 유형으로
사용해 쉐이더를 생성한다:
geometryShader = glCreateShader (GL_GEOMETRY_SHADER);
glShaderSource (geometryShader, 1, &gShaderCode, NULL);
glCompileShader (geometryShader);
...
glAttachShader (program, geometryShader);
glLinkProgram (program); 쉐이더 컴파일 코드는 기본적으로 정점 및 조각 쉐이더 코드와 동일하다. 컴파일 또는 링크 오류를 확인해라!
컴파일하고 실행하면 다음과 비슷한 결과가 나타난다:

기하학 쉐이더가 없는 경우와 완전히 같다. 약간은 어둡다. 하지만, 우리가 여전히 포인트를 그릴 수 있다는 사실은 기하학 쉐이더가 작동한다는
것을 의미하므로 이제는 더 펑키한 것들을 위한 시간이다.
Let's build some houses
점과 선을 그리는 것은 그다지 흥미롭지 않다. 그래서 우리는 기하학 쉐이더를 사용해 각 점의 위치에 우리를 위한 house를 그려서 조금
창의적으로 만들 것이다. 우리는 geometry shader의 출력을 triangle_strip으로 설정하고, 정사각형에 2개와 지붕 1개, 총 3개의 삼각형을
그려서 이 작업을 수행 할 수 있다.
OpenGL에서 삼각형 스트립은 보다 적은 정점을 사용해 삼각형을 그리는 보다 효율적인 방법이다. 첫 번째 삼각형이 그려지면 각 연속된
정점은 첫 번째 삼각형 옆에 또 다른 삼각형을 생성한다. 인접한 세 개의 꼭지점은 모두 삼각형을 형성한다. 우리가 삼각형 스트립을 형성하는
총 6개의 꼭지점을 가진다면 우리는 (1,2,3), (2,3,4), (3,4,5), (4,5,6) 총 4개의 삼각형을 형성한다. 삼각형 스트립은 적어도 3개의 정점이 필요하고
N-2개의 삼각형을 생성한다. 6개의 정점을 가지고 4개의 삼각형을 만들었다. 다음 이미지는 이를 설명한다:
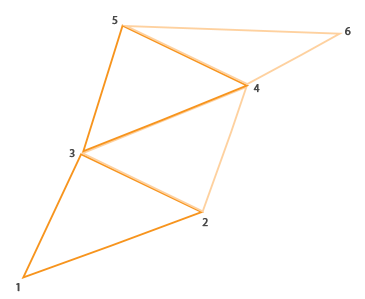
3차원 스트립을 기하학 쉐이더의 출력으로 사용하면 올바른 순서로 인접한 3개의 삼각형을 생성해 우리가 만들 집 모양을 쉽게 만들 수 있다.
다음 이미지는 파란색 점이 입력 점이 될 때 필요한 꼭지점을 그리는데 필요한 순서를 보여준다:
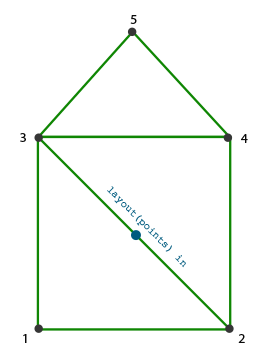
이것은 다음의 기하학 쉐이더로 변환된다:
#version 330 core
layout (points) in;
layout (triangle_strip, max_vertices = 5) out;
void build_house(vec4 position)
{
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1:bottom-left
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2:bottom-right
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3:top-left
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4:top-right
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5:top
EmitVertex();
EndPrimitive();
}
void main() {
build_house(gl_in[0].gl_Position);
} 이 기하학 쉐이더는 5개의 꼭지점을 생성한다. 각 꼭지점은 점의 위치에 오프셋을 더한 하나의 큰 삼각형 스트립을 형성한다.
그 결과 생성된 프리미티브는 래스터화되고 조각 쉐이더는 전체 삼각형 스트립에서 실행되어 그려진 각 지점에 대한 그린 하우스가 생성된다:
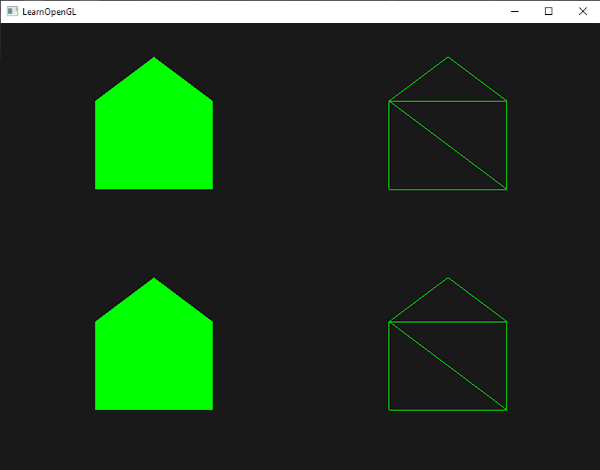
각 집은 사실 3개의 삼각형으로 구성되어 있으며 공간의 한 점을 사용해 그려져 있다. 그린 하우스는 약간 지루해보일지라도
각 하우스에 고유한 색상을 지정해 조금씩 활력을 북돋워준다. 이를 위해 정점 쉐이더에서 정점마다 색 정보를 가진 추가 정점 속성을 추가하고,
이를 쉐이더로 전달하는 기하학 쉐이더로 연결한다.
업데이트된 정점 데이터는 다음과 같다:
float points[] = {
-0.5f, 0.5f, 1.0f, 0.0f, 0.0f, // top-left
0.5f, 0.5f, 0.0f, 1.0f, 0.0f, // top-right
0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // bottom-right
-0.5f, -0.5f, 1.0f, 1.0f, 0.0f // bottom-left
}; 그런 다음 정점 쉐이더를 업데이트해 인터페이스 블록을 사용해 색상 속성을 기하학 쉐이더로 전달한다:
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;
out VS_OUT {
vec3 color;
} vs_out;
void main()
{
gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0);
vs_out.color = aColor;
} 그런 다음 기하학 쉐이더에서 동일한 인터페이스 블록을 선언해야한다 (인터페이스 이름은 다른):
in VS_OUT {
vec3 color;
} gs_in[]; 기하학 쉐이더는 일련의 정점을 입력으로 사용하기 때문에 정점 쉐이더의 입력 데이터는 지금 당장 하나의 정점만 가지고도
항상 데이터 배열로 표현된다.
in vec3 vColor[];
그런 다음 조각 쉐이더 단계에 대한 출력 컬러 벡터도 선언해야한다:
out vec3 fColor; 조각 쉐이더는 하나의 색상만을 필요로 하므로 여러 색상을 전달하는 것은 의미가 없다. 따라서 fColor 벡터는 배열이 아니라
단일 벡터이다. 정점을 방출 할 때, 각 정점은 조각 쉐이더 실행을 위해 fColor에 마지막 저장된 값을 저장한다.
집에서는 처음 정점이 전체 집 색상을 지정하기 전에 먼저 정점 쉐이더의 색상으로 fColor를 채울 수 있다:
fColor = gs_in[0].color; // gs_in[0] since there's only one input vertex
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1:bottom-left
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2:bottom-right
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3:top-left
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4:top-right
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5:top
EmitVertex();
EndPrimitive(); 생성된 모든 정점은 데이터에 포함된 fColor의 마지막 저장된 값을 갖는다. 이 값은 해당 속성에서 정의한 정점 색상과 같다.
모든 집은 지금 그들 자신의 색깔을 가질 것이다:
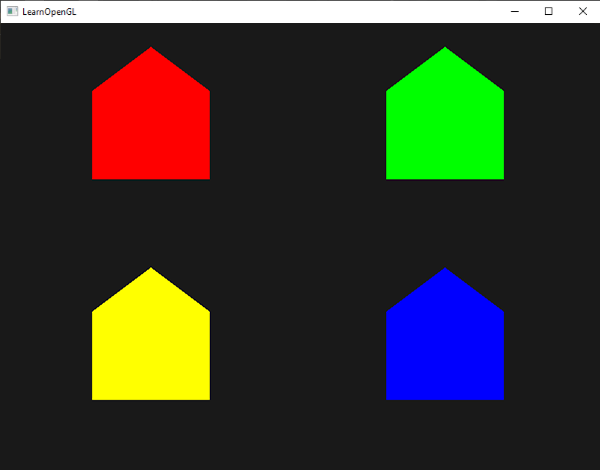
단지 재미로 우리는 겨울임을 가장해 마지막 꼭지점에 흰색의 색을 부여해 지붕에 약간의 눈을 내릴 수도 있다.
fColor = gs_in[0].color;
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1:bottom-left
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2:bottom-right
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3:top-left
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4:top-right
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5:top
fColor = vec3(1.0, 1.0, 1.0);
EmitVertex();
EndPrimitive(); 결과는 다음과 같다:
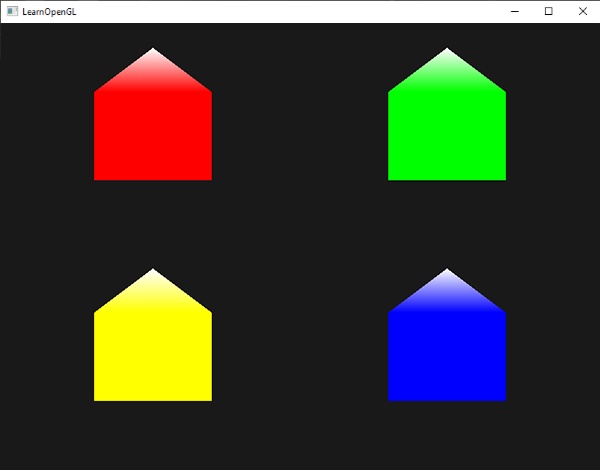
기하학 쉐이더를 사용하면 가장 간단한 프리미티브로도 매우 독창적인 작업을 수행 할 수 있다. shape가 GPU의 초고속 하드웨어에서
동적으로 생성되기 때문에 이 모양을 정점 버퍼 내에서 직접 정의하는 것보다 훨씬 효율적이다. 따라서 기하학 버퍼는 voxel 세계의 큐브와
같은 자주 반복되는 단순한 모양이나 커다란 야외 필드의 잔디 잎에서 최적화를 위한 훌륭한 도구이다.
Exploding objects
집을 그리는 것은 재미있지만 그렇게 많이 사용하지 않는다. 그래서 우리는 이제 그것을 한 단계 높이고 물체를 폭발시킬 것이다.
그것은 우리가 그다지 많이 사용하지는 않을 것이지만 기하학 쉐이더의 힘을 보여준다.
우리가 객체를 폭발시킬 때 우리는 실제로 귀중한 번들된 정점 세트를 날려 버리지는 않을 것이다. 그러나 우리는 작은 시간 동안
그들의 법선 벡터의 방향을 따라 각각의 삼각형을 움직일 것이다. 결과는 전체 객체의 삼각형이 삼각형의 법선 벡터의 방향을 따라
폭발하는 것처럼 보인다. nanosuit 모델에서 삼각형을 폭발시키는 효과는 다음과 같다:
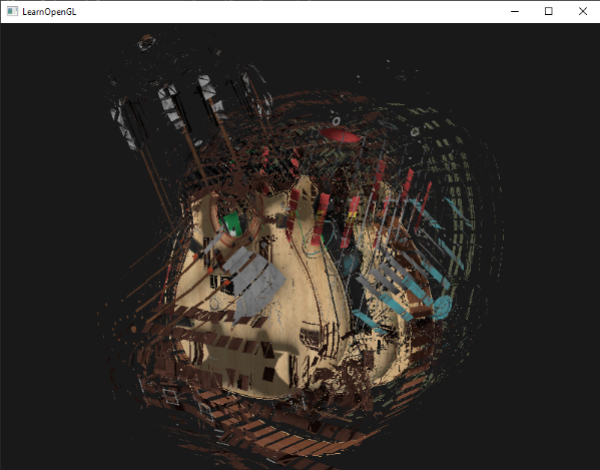
이러한 기하학 쉐이더 효과의 장점은 복잡성에 관계없이 모든 개체에서 작동한다는 것이다.
각 꼭지점을 삼각형의 법선 벡터의 방향으로 변환 할 것이기 때문에 먼저 이 법선 벡터를 계산해야한다. 우리가 해야 할 것은 우리가
접근 할 수 있는 꼭지점 3개를 사용해 삼각형의 표면에 수직인 벡터를 계산하는 것이다. transformations 튜토리얼에서 교차 곱을
사용해 두 개의 다른 벡터에 수직인 벡터를 검색 할 수 있다는 것을 기억할 것이다. 삼각형의 표면에 평행한 두 개의 벡터 a와 b를
검색한다면 해당 벡터에 대해 교차 곱을 수행해 법선 벡터를 검색 할 수 있다. 다음의 쉐이더 함수는 이것을 정확히 수행해
3개의 입력 정점 좌표를 사용해 법선 벡터를 검색한다:
vec3 GetNormal()
{
vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
return normalize(cross(a, b));
} 여기서 우리는 감산을 사용해 삼각형의 표면에 평행한 두 개의 벡터 a와 b를 검색한다. 서로 다른 두 벡터를 빼면 두 벡터의 차이 벡터가 생기고
삼각형 평면에 있는 모든 세 점은 서로의 벡터를 뺀 값이 평면에 평행한 벡터가 된다. 교차 함수에서 a와 b를 바꾸면 반대 방향을 가리키는
법선 벡터를 얻을 수 있다.
이제는 법선 벡터를 계산하는 방법을 알았으므로 이 법선 벡터를 정점 위치 벡터와 함께 사용하는 분해 함수를 만들 수 있다.
이 함수는 법선 벡터의 방향을 따라 위치 벡터를 변환하는 새 벡터를 반환한다:
vec4 explode(vec4 position, vec3 normal)
{
float magnitude = 2.0;
vec3 direction = normal * ((sin(time) + 1.0) / 2.0) * magnitude;
return position + vec4(direction, 0.0);
} 함수 자체가 너무 복잡해서는 안 된다. sin 함수는 시간을 기반으로 -1.0과 1.0 사이의 값을 반환하는 인수로 시간 변수를 받는다.
우리가 물체를 내파하고 싶지 않기 때문에 sin 값을 [0,1] 범위로 변환한다. 결과 값에 법선 벡터가 곱해지고 결과 방향 벡터가
위치 벡터에 추가된다.
모델 로더를 사용해 로드된 모델을 그리는 동안 폭발 효과를 위한 완벽한 기하학 쉐이더는 다음과 같다:
#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices = 3) out;
in VS_OUT {
vec2 texCoords;
} gs_in[];
out vec2 TexCoords;
uniform float time;
vec4 explode(vec4 position, vec3 normal) { ... }
vec3 GetNormal() { ... }
void main() {
vec3 normal = GetNormal();
gl_Position = explode(gl_in[0].gl_Position, normal);
TexCoords = gs_in[0].texCoords;
EmitVertex();
gl_Position = explode(gl_in[1].gl_Position, normal);
TexCoords = gs_in[1].texCoords;
EmitVertex();
gl_Position = explode(gl_in[2].gl_Position, normal);
TexCoords = gs_in[2].texCoords;
EmitVertex();
EndPrimitive();
} 정점을 방출하기 전에 적절한 텍스처 좌표를 출력한다는 점에 유의해라.
또한, 실제로 OpenGL 코드에서 시간 변수를 설정하는 것을 잊지 말아라:
shader.setFloat("time", glfwGetTime ()); 결과적으로 시간이 지남에 따라 정점이 계속 폭발해 다시 정상으로 돌아오는 3D 모델이 생성된다. 정확하게 유용하지는 않지만
기하학 쉐이더의 고급 사용법을 보여준다.
Visualizing normal vectors
이 섹션에서는 실제로 유용하게 사용 할 수 있는 기하학 쉐이더를 사용하는 예제를 제공한다. 모든 오브젝트의 법선 벡터를 시각화하는 것이다.
조명 쉐이더를 프로그래밍 할 때 궁극적으로 이상한 시각적 출력으로 연결되어 원인을 파악하기 어렵다. 조명 오류의 일반적인 원인은 부정확하게
정점 데이터를 로드하거나 정점 속성으로 부적절하게 지정하거나 쉐이더에서 잘못 관리해 발생하는 잘못된 법선 벡터가 문제이다.
우리가 원하는 것은 우리가 제공하는 법선 벡터가 정확한지를 검출 할 수 있는 방법이다.
법선 벡터가 올바른지 판단하는 가장 좋은 방법은 시각화하는 것이다. 기하학 쉐이더가 이 목적을 위해 매우 유용한 도구이다.
아이디어는 다음과 같다. 우리는 처음에 기하학 쉐이더가 없는 장면을 보통으로 그린 다음 두 번째 장면을 그린다.
두 번째 장면에서는 기하학 쉐이더를 통해 생성하는 법선 벡터만 표시한다. 기하학 쉐이더는 삼각형 프리미티브를 입력으로 가져와서
법선 벡터의 방향에서 3개의 선을 생성한다. 즉, 각 정점에 대한 하나의 법선 벡터이다. 의사 코드에서는 다음과 같이 보일 것이다:
shader.use();
DrawScene();
normalDisplayShader.use();
DrawScene();이번에는 모델에서 제공한 정점 법선을 사용해 모델을 생성하는 대신에 쉐이더를 만든다. 스케일과 회전을 수용하기 위해
법선을 먼저 클립 공간 좌표로 변환하기 전에 법선을 변형한다. 이것은 정점 쉐이더에서 모두 수행 할 수 있다:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
out VS_OUT {
vec3 normal;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
mat3 normalMatrix = mat3(transpose(inverse(view * model)));
vs_out.normal = normalize(vec3(projection * vec4(normalMatrix * aNormal, 0.0)));
}변환된 클립 공간 수직 벡터는 인터페이스 블록을 통해 다음 쉐이더 스테이지로 전달된다. 그 다음 기하학 쉐이더는 각 꼭지점을
가져와서 각 위치 벡터에서 법선 벡터를 그린다:
#version 330 core
layout (triangles) in;
layout (line_strip, max_vertices = 6) out;
in VS_OUT {
vec3 normal;
} gs_in[];
const float MAGNITUDE = 0.4;
void GenerateLine(int index)
{
gl_Position = gl_in[index].gl_Position;
EmitVertex();
gl_Position = gl_in[index].gl_Position + vec4(gs_in[index].normal, 0.0) * MAGNITUDE;
EmitVertex();
EndPrimitive();
}
void main()
{
GenerateLine(0); // first vertex normal
GenerateLine(1); // second vertex normal
GenerateLine(2); // third vertex normal
} 이와 같은 기하학 쉐이더의 내용은 지금 당장은 자명하다. 표시된 법선 벡터의 크기를 제한하기 위해 법선 벡터에 MAGNITUDE 벡터를
곱하는 것이다.
시각화 법선은 주로 디버깅 목적으로 사용되기 때문에 조각 쉐이더의 도움을 받아 단색의 라인으로 표시 할 수 있다:
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(1.0, 1.0, 0.0, 1.0);
} 이제 정상 쉐이더로 모델을 렌더링 한 다음 특별 정상 쉐이딩 쉐이더로 다음과 같이 보일 것이다:
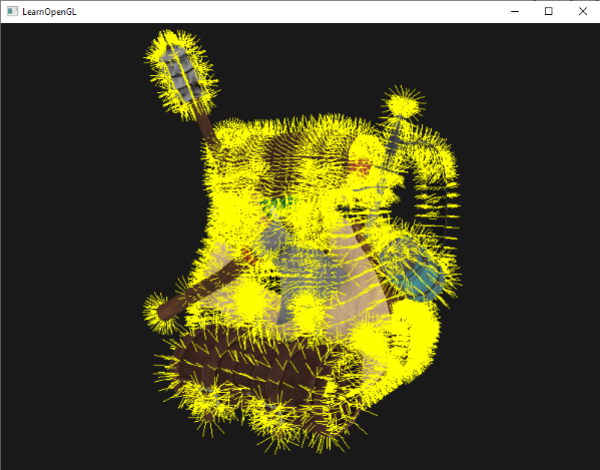
이것은 모델의 법선 벡터가 실제로 올바른지를 결정하는데 정말 유용한 방법을 제공한다. 이와 같은 기하학 쉐이더가
모피를 오브젝트에 추가하는 등에도 사용된다고 생각할 수 있다.
** ** ** ** ** ** ** ** ** **
오늘 물리 공부하다가 링크 오류떠서 OpenGL 공부 먼저 했다. 후~~ 쪼끔 쉬었다가 저녁에 물리 공부해야지!
'Game > Graphics' 카테고리의 다른 글
| Learn OpenGL - Advanced OpenGL : Anti Aliasing (0) | 2018.09.11 |
|---|---|
| Learn OpenGL - Advanced OpenGL : Instancing (0) | 2018.09.10 |
| Learn OpenGL - Advanced OpenGL : Advanced GLSL (0) | 2018.09.08 |
| LearnOpenGL - Advanced OpenGL : Advanced Data (0) | 2018.09.07 |
| Learn OpenGL - Advanced OpenGL : Cubemaps (0) | 2018.09.06 |

