link : https://learnopengl.com/Advanced-OpenGL/Depth-testing
Depth testing
Coordinate systems 튜토리얼에서 우리는 3D 컨테이너를 렌더링하고 깊이 버퍼를 사용해 다른면
뒤에 있는 동안 face 렌더링을 앞쪽으로 방지한다. 이 튜토리얼에서는 깊이 버퍼가 저장하는 이러한
깊이 값과 실제로 조각이 다른 조각 뒤에 있는지 여부를 실제로 결정하는 방법에 대해 자세히 설명한다.
깊이 버퍼는 색상 버퍼 (모든 조각 색상을 저장하는 : 시각적 출력)와 마찬가지로 단편마다 정보를 저장하고
색상 버퍼와 동일한 너비와 높이를 갖는 버퍼이다. 깊이 버퍼는 윈도우 시스템에 의해 자동으로 생성되며
깊이 값은 16, 24, 32 비트 부동 소수점으로 저장된다. 대부분의 시스템에서는 정밀도가 24비트인 깊이 버퍼가 표시된다.
깊이 테스트가 활성화되면 OpenGL은 깊이 버퍼의 내용에 대해 프래그먼트의 깊이 값을 테스트한다.
OpenGL은 깊이 테스트를 수행하고 이 테스트가 통과하면 깊이 버퍼가 새 깊이 값으로 업데이트된다.
깊이 테스트가 실패하면 조각을 버린다.
깊이 테스트는 프래그먼트 쉐이더가 실행된 후 스크린 공간에서 수행된다. 스크린 공간 좌표는 OpenGL의 glViewport 함수에
의해 정의되는 표시 영역과 직접 관련 프래그먼트 쉐이더 GLSL의 내장 gl_FragCoord 변수를 통해 액세스 될 수 있다.
gl_FragCoord의 x 및 y 구성 요소는 프래그먼트의 화면 공간 좌표를 나타낸다. ( (0,0)은 왼쪽 하단 모서리이다)
gl_FragCoord는 조각의 실제 깊이를 포함하는 z-구성 요소도 포함한다. 이 z 값은 깊이 버퍼의 내용과 비교되는 값이다.
조각 쉐이더는 일반적으로 비용이 비싸다. 따라서 우리가 어디에서 실행해야하는지 피할 수 있다. 초기 기핑 테스트를 위한 프래그먼트 쉐이더에 대한 제한은 프래그먼트의 깊이 값에 쓰지 말아야한다는 것이다. 프래그먼트 쉐이더가 깊이 값에 쓰면 초기 깊이 테스트가 불가능하다. OpenGL은 깊이 값을 미리 파악할 수 없다.
깊이 테스트는 기본적으로 비활성화되어 있으므로 깊이 테스트를 사용하려면 GL_DEPTH_TEST 옵션을 사용해 깊이 테스트를 활성화 해야한다:
glEnable (GL_DEPTH_TEST); 일단 활성화되면 OpenGL은 깊이 테스트를 통과하면 깊이 버퍼에 z-값을 자동으로 저장하고, 그에 따라 깊이 테스트에 실패하면 조각을 버린다.
깊이 테스트가 가능하다면 GL_DEPTH_BUFFER_BIT를 사용해 각 렌더링 반복 전에 깊이 버퍼를 지워야한다. 그렇지 않으면 마지막 렌더링 반복에서
작성된 깊이 값이 붙어있게 된다:
glClear (GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); 모든 조각에 대해 깊이 테스트를 수행하고 그에 따라 적절하게 버리고 싶지만, 깊이 버퍼를 업데이트하지 않으려는 경우가 있다.
기본적으로 당신은 읽기 전용 깊이 버퍼를 사용하고 있다. OpenGL을 사용하면 깊이 마스크를 GL_FALSE로 설정해 깊이 버퍼에
쓰지 못하게 할 수 있다:
glDepthMask (GL_FALSE); 깊이 테스트가 활성화된 경우에만 효과가 있다.
Depth test function
OpenGL을 사용하면 깊이 테스트에 사용되는 비교 연산자를 수정할 수 있다. 이를 통해 OpenGL이 조각을 전달하거나
폐기해야하는 시점과 깊이 버퍼를 업데이트해야하는 시점을 제어할 수 있다. glDepthFunc를 호출해 비교 연산자를 설정할 수 있다:
glDepthFunc (GL_LESS); 이 함수는 아래 표에 나열된 몇 가지 비교 연산자를 사용할 수 있다:
| Function | Description |
|---|---|
GL_ALWAYS | The depth test always passes. |
GL_NEVER | The depth test never passes. |
GL_LESS | Passes if the fragment's depth value is less than the stored depth value. |
GL_EQUAL | Passes if the fragment's depth value is equal to the stored depth value. |
GL_LEQUAL | Passes if the fragment's depth value is less than or equal to the stored depth value. |
GL_GREATER | Passes if the fragment's depth value is greater than the stored depth value. |
GL_NOTEQUAL | Passes if the fragment's depth value is not equal to the stored depth value. |
GL_GEQUAL | Passes if the fragment's depth value is greater than or equal to the stored depth value. |
기본적으로 깊이 함수 GL_LESS는 현재 깊이 버퍼의 값보다 높은 값을 가진 모든 조각을 버리는데 사용된다.
깊이 함수를 변경하면 시각적 출력에 미치는 영향을 보여준다. 조명이 없는 텍스처 바닥에 두 개의 큐브가 있는
기본 장면을 표시하는 새로운 코드 설정을 사용한다.
소스 코드에서 깊이 함수를 GL_ALWAYS로 변경했다.
glEnable (GL_DEPTH_TEST);
glDepthFunc (GL_ALWAYS); 이것은 깊이 테스트를 활성화하지 않은 경우와 동일한 동작을 시뮬레이션한다. 깊이 테스트는 항상 단순히 통과하므로
마지막에 그려진 단편은 앞에 있어야 했음에도 불구하고 그려진 단편 앞에 렌더링된다. 바닥 평면을 마지막으로 그려서
평면의 파편이 각 컨테이너 조각을 덮어 쓴다.
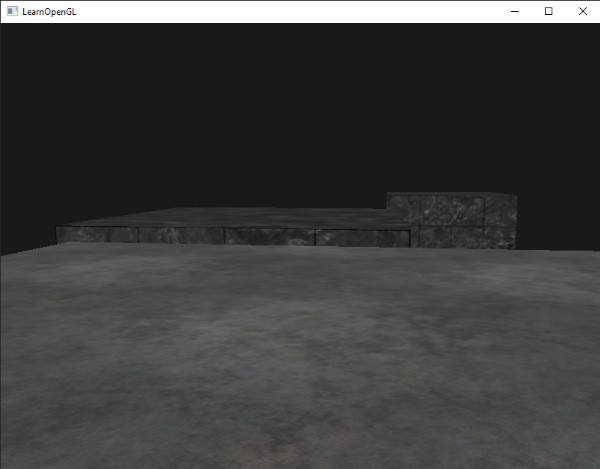
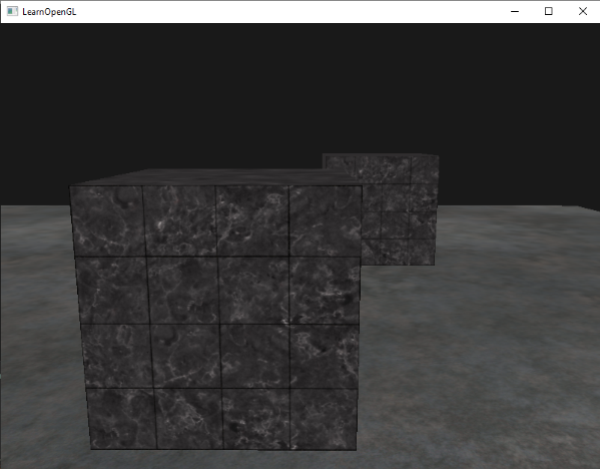
모두 다시 GL_LESS로 설정하면 익숙한 장면 유형이 생긴다:
Depth value precision
깊이 버퍼는 0.0과 1.0 사이의 깊이 값을 포함하며 뷰어에서 보았을 때 장면의 모든 객체의 z값과 해당 내용을 비교한다.
뷰 공간에서 이러한 z값은 projection frustum의 근사치와 근사치 사이의 값이 될 수 있다.
따라서 우리는 이러한 뷰 공간 z 값을 [0,1]의 범위로 변환할 방법이 필요하며 한 가지 방법은 [0,1] 범위로 선형 변환하는 것이다.
다음 (선형) 방정식은 z값을 0.0과 1.0 사이의 깊이 값으로 변환한다.
near과 far는 투영 행렬에 가시적인 frustum을 설정하기 위해 설정된 near과 far 값이다.
**절두체 : 어떤 물체를 그 밑면과 평행하는 평면으로 자를 때 그 밑면과 평면 사이의 부분)
이 방정식은 절두체 내의 깊이 값 z를 취해 범위 [0,1]로 변환한다. z값과 해당 깊이 값 사이의 관계는 다음 그래프에 표시된다:
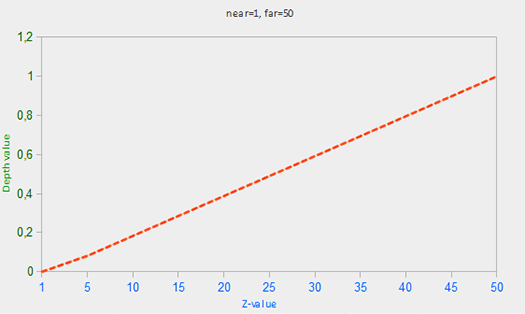
그러나 실제로는 이와 같은 선형 깊이 버퍼는 거의 사용되지 않는다. 올바른 투영 속성의 경우 1/z에 비례하는 비선형 깊이 방정식이
사용된다. 이것이 기본적으로 하는 일은 z가 작을 때 엄청난 정밀도를 제공하고, z가 멀리 있을 때 정확성을 줄인다. 이것을 잠시
생각해보아라: 1000단위 떨어져 있는 깊이 값이 1의 거리에 있는 매우 상세한 오브젝트와 같은 정밀도를 가지기를 원하나?
선형 방정식은 이것을 고려하지 않는다.
비선형 함수가 1/z에 비례하기 때문에 예를 들어 1.0과 2.0사이의 z값은 1.0과 0.5사이의 깊이 값을 발생시킨다.
이는 float가 제공하는 정밀도의 절반이므로 작은 z축에서 엄청난 정밀도를 제공한다. 값 50.0과 100.0 사이의 z 값은
float의 정밀도의 2%만 차지한다. 이는 정확히 우리가 원하는 것이다. 가까운 거리와 먼 거리를 고려한 이러한 방정식은 다음과 같다:
이 방정식으로 어떤 일이 벌어지고 있는지 정확히 알지 못한다고 걱정하지 말아라. 기억해야할 중요한 점은 깊이 버퍼의 값이
스크린 공간에서 선형적이지 않다는 것이다. 깊이 버퍼에서 0.5의 값은 절두체에서 객체의 z값이 중간에 있음을 의미하지는 않는다.
정점의 z값은 실제로 가까운 평면에 아주 가깝다! 다음 그래프에서 z값과 결과 버퍼의 값 사이의 비선형 관게를 볼 수 있다:
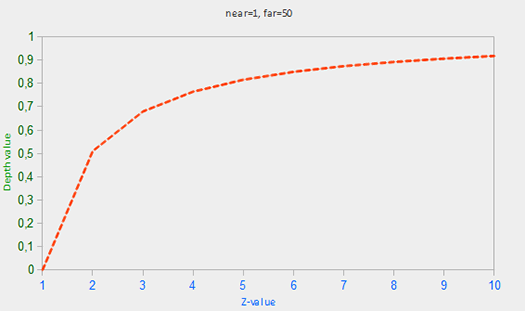
보시다시피 깊이 값은 작은 z값에 의해 크게 결정되므로 가까이 있는 물체에 엄청난 깊이 정밀도를 부여한다.
뷰어의 관점에서 z값을 변환하는 방정식은 투영 행렬에 포함되어 있으므로 뷰에서 클립으로 그리고 스크린 공간에서
정점 좌표를 변환할 때 비선형 방정식이 적용된다. 투영 행렬이 실제로 무엇을 하는지 궁금하다면 이 기사를 참조해라.
깊이 버퍼를 시각화하려고하면 이 비선형 수식의 효과가 빠르게 나타난다.
Visualizing the depth buffer
프래그먼트 쉐이더에 내장된 gl_FragCoord 벡터의 z값은 특정 프래그먼트의 깊이 값을 포함한다는 것을 알고 있다.
이 조각의 깊이 값을 색상으로 출력한다면 장면의 모든 조각의 깊이 값을 표시할 수 있다.
프래그먼트의 깊이 값에 따라 색상 벡터를 반환하면된다:
void main()
{
FragColor = vec4(vec3(gl_FragCoord.z), 1.0);
} 그런 다음 동일한 프로그램을 다시 실행하면 모든 것이 흰색이 되어 모든 심도 값인 1.0임을 알 수 있다.
그렇다면 왜 깊이 값이 0.0에 더 가깝고 더 어두워지지 않는 이유는 무엇일까?
이전 섹션에서 화면 공간의 깊이 값이 비선형임을 예를 들어 기억할 수 있다. 그들은 작은 z-값에 대해서는 매우 높은 정밀도를,
큰 z-값에 대해서는 낮은 정밀도를 갖는다. 조각의 깊이 값은 거리에 따라 빠르게 증가하므로 거의 모든 꼭지점의 값이 1.0에 가깝다.
조심스럽게 물체 가까이에서 움직이면 색이 어두워지는 것을 볼 수 있으며 z값이 점점 작아지는 것을 알 수 있다:
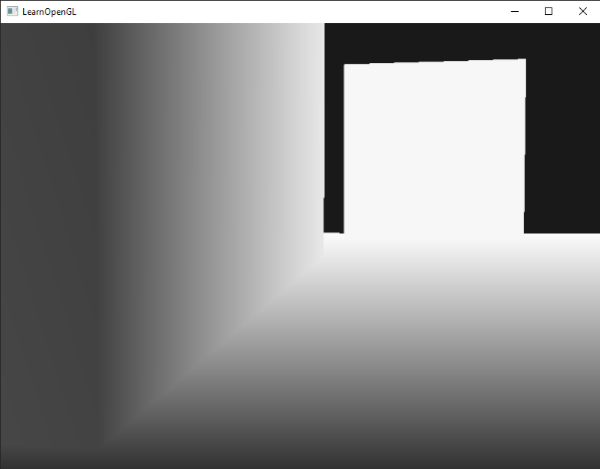
이것은 깊이 값의 비선형성을 명확하게 보여준다. 가까운 객체는 멀리있는 객체보다 깊이 값에 훨씬 큰 영향을 미친다.
몇인치만 움직이면 어두운 색에서 완전히 흰색으로 변한다.
그러나 프래그먼트의 비선형 깊이 값을 선형 형제로 다시 변환할 수 있다. 이를 달성하기 위해서는 기본적으로 깊이 값만을 위한
투영 과정을 역전해야한다. 즉, 범위 값 [0,1]에서 범위 [-1,1]의 표준화 장치 좌표로 깊이 값을 다시 변환해야 함을 의미한다.
그런 다음 투영 행렬에서와 같이 비선형 방정식을 뒤집어 결과 깊이 값에 이 역방정식을 적용하려고 한다.
결과는 선형 깊이 값이다.
먼저 깊이 값을 너무 어렵지 않은 NDC로 변환하려고한다:
float z = depth * 2.0 - 1.0; 그런 다음 결과 z값을 가져와서 역변환을 적용해 선형 깊이 값을 검색한다:
float linearDepth = (2.0 * near * far) / (far + near - z * (far - near)); 이 방정식은 near과 far 사이의 깊이 값을 반환하는 깊이 값을 비선형화하기 위해 방정식 2를 다시 사용하는 투영 행렬로부터 유ㅗㄷ된다.
이 무거운 수학 기사는 거대한 세부사항에 흥미있는 독자를 위한 투영 행렬을 설명한다.
화면 공간의 비선형 깊이를 선형 깊이 값으로 변환하는 완벽한 프래그먼트 쉐이더는 다음과 같다:
#version 330 core
out vec4 FragColor;
float near = 0.1;
float far = 100.0;
float LinearizeDepth(float depth)
{
float z = depth * 2.0 - 1.0; // back to NDC
return (2.0 * near * far) / (far + near - z * (far - near));
}
void main()
{
float depth = LinearizeDepth(gl_FragCoord.z) / far; // divide by far for demonstration
FragColor = vec4(vec3(depth), 1.0);
}선형화된 깊이 값의 범위는 near에서 far까지의 값이 대부분 1.0보다 커서 완전히 흰색으로 표시된다.
주 함수에서 선형 깊이 값을 멀리 나누면 선형 깊이 값을 대략 [0,1] 범위로 변환한다. 이렇게하면 조각이 투영 절두체의
먼 평면에 가까울수록 장면이 밝아지는 것을 점차 볼 수 있다. 이는 데모 목적에 더 적합하다.
이제 우리가 응용 프로그램을 실행하면 거리에 대해 선형적인 깊이 값을 얻는다. 장면 주위를 이동해 심도 값이 선형으로 변하는지 확인해라:
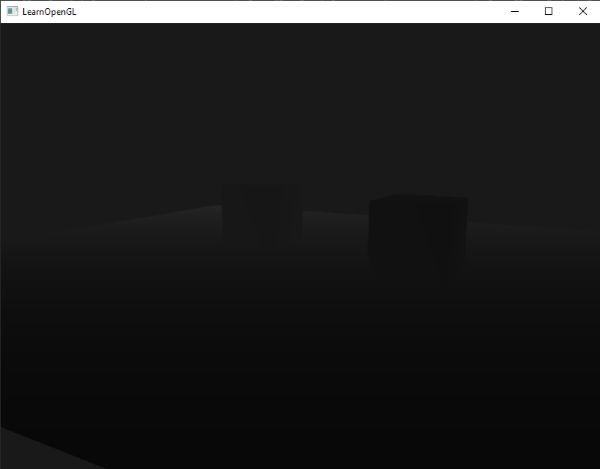
깊이 값은 근거리 평면에서 0.1까지 원거리 평면에 선형적으로 분포하기 때문에 색상은 대부분 검정색이다.
멀리 있는 평면은 여전히 우리에게서 멀리 떨어져 있다. 결과적으로 우리는 가까운 평면에 비교적 가깝고 더 어두운 깊이 값을 얻는다.
Z-fighting
두 개의 평면 또는 삼각형이 서로 너무 가깝게 정렬되어 깊이 버퍼에 두 도형 중 어느 것이 다른 정면에 있는지를 알아내기에
충분한 정밀도가 없는 경우 일반적인 시각적 아티팩트(인공물)가 발생할 수 있다. 결과적으로 두 모양이 지속적으로 이상한
글리치 패턴을 일으키는 순서를 전환하는 것처럼 보인다. 이 모양은 z-fighting이라고 한다. 왜냐하면 도형이 위로
올라오고 싸우는 것처럼 보이기 때문이다.
지금까지 사용해온 장면에서 z-fighting이 꽤 두드러지는 지점이 있다. 컨테이너는 바닥이 놓인 정확한 높이에 놓였는데
이는 컨테이너의 바닥 평면이 바닥 평면과 동일 평면상에 있음을 의미한다. 두 평면의 깊이 값은 동일하므로 결과 깊이 테스트에서
어느 것이 올바른 것인지를 알아낼 방법이 없다.
효과를 명확하게 볼 수 있는 컨테이너 중 하나에서 카메라를 이동하면 컨테이너의 하단 부분이 컨테이너 평면과 바닥 평면 사이를
끊임없이 지그재그 패턴으로 전환한다.
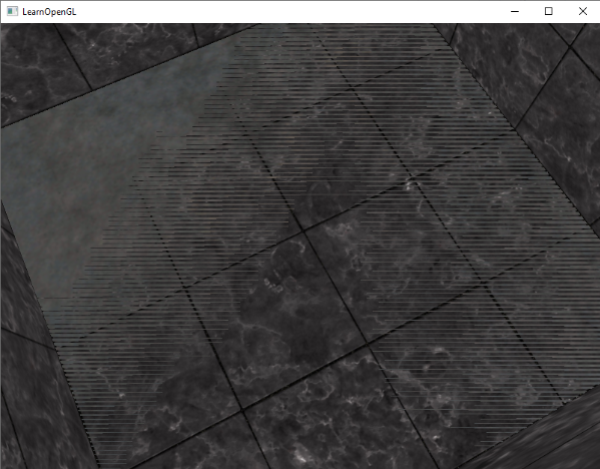
Z-fighting은 깊이 버퍼의 공통적인 문제이며 오브젝트가 먼 거리에 있을 때 (깊이 버퍼가 더 큰 z값에서 덜 정밀하기 때문)
일반적으로 더 강력하다. z-fighting을 완전히 막을 수는 없지만 일반적으로 장면에서 z-fighting을 완화하거나 완전히
예방하는데 도움이 되는 몇가지 트릭이 있다.
Prevent z-fighting
가장 중요한 첫 번째 트릭은 오브젝트를 서로 너무 가깝게 두지 않아서 삼각형의 일부가 서로 겹치지 않도록 하는 것이다.
사용자가 거의 눈에 띄지 않는 두 객체 사이에 작은 간격 띄우기를 생성하면 두 객체간에 z-fighting을 완전히 제거할 수 있다.
컨테이너와 바닥의 경우 컨테이너를 양의 y 방향으로 약간 움직일 수 있었다. 컨테이너 위치의 작은 변화는 전혀 눈에 띄지
않을 것이고, z-fighting을 완전히 줄인다. 그러나 이 작업을 위해서는 각 물체를 수동으로 개입시켜야하며 씬의 어떤 물체도
z-fighting을 생성하지 않도록 철저한 테스트가 필요하다.
두 번째 트릭은 가까운 평면을 최대한 멀리 설정하는 것이다. 이전 섹션 중 하나에서 우리는 근사 평면 가까이에 있을 때
정밀도가 매우 크다고 설명했으므로 가까운 평면을 뷰어에서 멀리 이동하면 전체 절두체 범위에 대해 훨씬 더 높은 정밀도를
갖게 된다. 그러나 가까운 평면을 너무 멀리 설정하면 가까운 물체가 잘릴 수 있으므로 일반적으로 장면의 가장 가까운 거리를
파악하는 것은 조정 및 실험의 문제이다.
성능을 저하시키면서 또 다른 위대한 트릭은 더 높은 정밀도의 깊이 버퍼를 사용하는 것이다. 대부분의 깊이 버퍼는 24비트의
정밀도를 가지지만, 요즘 대부분의 카드는 32비트 깊이 버퍼를 지원해 상당한 양의 정밀도를 증가시킨다. 따라서 약간의 성능
비용으로 깊이 테스트를 통해 훨씬 더 정밀하게 z-fighting을 줄일 수 있다.
우리가 논의한 3가지 기술은 가장 일반적이며 적용하기 쉬운 z 방지 기술이다. 거기에 더 많은 작업이 필요하고 여전히 z-fighting을
완전히 비활성화하지 않는 몇 가지 다른 기술이 있다. z-fighting은 일반적인 문제이지만 나열된 기술의 적절한 조합을 사용하면
실제로 z-fighting을 다룰 필요가 없을 것이다.
** ** ** ** ** ** ** ** ** **
이상한 공식이 나와서 당황했지만 완벽히 알 필요는 없고, 이해하고 넘어가면 된다고 해서 다행이다.
커브미션을 제작할 때도 멀고 가까움을 조절해서 맵을 배치했었는데 그 생각이 다시 들었다.
다음 내용으로 고고
'Game > Graphics' 카테고리의 다른 글
| LearnOpenGL - Advanced OpenGL : Blending (0) | 2018.09.03 |
|---|---|
| Learn OpenGL - Advanced OpenGL : Stencil testing (0) | 2018.09.02 |
| Learn OpenGL - Model Loading : Model (0) | 2018.08.30 |
| Learn OpenGL - Model Loading : Mesh (0) | 2018.08.27 |
| Learn OpenGL - Model Loading : Assimp (0) | 2018.08.24 |


